一道八百年松鼠难题

中得到验证，这里的两个斐波纳契数分别为21和34。可惜小时候从向日葵上扣瓜子的经历，既没有变作大脑里的数学，也没有变成眼里的美，倒是化作了门牙上那个豁口。
　　

　　用同样方式体现斐波纳契数列的还有如下“菜市场系列”，你总是能在这些圆鼓鼓的表面上发现顺反两组螺旋，二者数目在一串有名的数列中互为左邻右舍，比如图中松果是8和13，菜花是5和8。所以，每当进入菜市场，你其实已经卷入了一场斐波纳契狂舞。
　　

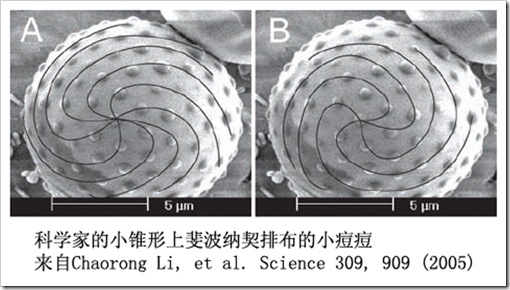
　　果实的斐波纳契排布本属生物问题，然而它的解答却在一个中国的物理实验室现出端倪。科学家做出一些非常微小的凸起，用软软的银做核心，用坚硬的二氧化硅做外壳，当小凸起遭到快速冷却，坚硬外壳就会受到均匀拉扯……（此处省去千余字，见下图）从而莫名其妙地在没有生命的小凸上长出无数小痘痘，自动排成向日葵瓜子的阵列。这种排布体现了对能量的最低要求，还能同时保证小痘痘等距排列。结论是，向日葵头和菊花头不想减肥，所以从来不会费很大力气地把自己长成有棱角的方脸，然后将种子码成方阵；它们一致喜欢的则是平滑的圆锥形脸，并让脸上的小痘痘长成两个斐波纳契数的螺旋组，这不光最省体力，而且还能保证你吃到的瓜子既饱满又等大。
　　
　　井井有条的习惯固然不可多得，但是人乱七八糟同样可以活得很好；至于植物何以固执地摒弃无序、通过上万年突变的积累进化出一张完美的数学脸，我只能叹一句“神奇”作为回应。
　　

　　当然，植物也有不喜欢圆锥脸庞的，另一个选择就是干脆长成四面八方都一样的圆球形，小痘痘在圆锥表面那扭曲的斐波纳契排布显然不满足球形那精美的辐射对称性，于是便排成了矢车菊那样的等距六边形。
　　

　　一次一个美国人给了我一颗草莓，我忍着强烈的饥饿将它供在了锥形瓶上。除了对转基因和农药心有余悸，原来也是源自我对美的一种下意识敏感。不管味道如何，草莓好歹得是个圆锥形，小粒粒的种子需以斐波纳契模式来排布；但是在这颗可怜的草莓上，广大的面积却是马蹄、平面等等诡异的形状，以至于斐波纳契只在角落苟延残踹。现在，科学家告诉我们，在受刺激（frustrated）的表面上会形成X形排布——幸好我当时留下照片为证。
　　

　　有人有疑问，上文所说的菜花和松果究竟是怎么画出几个圈圈来的，请见下图（顺便附送我在北京照的大斐波纳契套小斐波纳契的菜花花）～
　　

来源：科学松鼠会
　　
　　

上一页 [1] [2]