这次来谈谈拓扑学中有代表性的一个课题,扭结分类问题。所谓扭结,顾名思义就是一根绳子首尾相接,它可能打了结。更一般的,可以是几根绳子,除了自身打结以外,还互相打结。对具体的一个扭结,也许可以通过做实验的办法判断它是否打结,但是数学家希望找一个普适的,定量的办法。比如说,任意画一个扭结(它实际上是一个空间扭结的平面投影),比如这个有点复杂的,怎样不动手做实验就能判断它到底有没有打结?

这个问题后来证实是非常复杂的问题。在有了计算机以后,才能找到一种时间代价很高的算法让计算机帮助我们判断一个扭结投影到底有没有打结。直到2006年,才找到一种真正快速的计算机算法来判断这件事。
扭结分类的问题比判断是否打结更困难。比如,以下两个扭结都打了结,它们是否本质上是同一种结?

所谓“分类”,就是要找一个(可计算的)判据,使得当两个扭结满足这个判据时就是同一种结;当它们不满足这个判据时就不是同一种结。到现在为止,也还只能找到一些非常复杂的判据,同样要借助计算机才能大致判断两个扭结是否本质上为同一种结。
扭结理论有一段很有趣的早期历史。1867年,著名物理学家开尔文勋爵,就是那个号称物理学已经接近终结,只剩“两朵乌云”的开尔文,突然产生了关于化学元素表的新看法(那时候还没有发现原子,所以化学元素表还是一个谜)。开尔文认为,不同的化学元素其实是“以太”的涡旋在空间中的扭结形态。“以太”是19世纪的物理学家们发明的概念,它被想象成充满整个空间,是电磁波传播的载体(或媒质)。开尔文是很严肃的物理学家,当然不能凭空想象,实际上他提出了几个即使从现在的观点看来也很合理的证据:
(1)元素很稳定,这可以用扭结的拓扑性质来解释,微小的形变不改变扭结的“扭法”。
(2)元素很多样,这可以用扭结的多样性来解释,不同的“打结方式”实在太多了。
(3)不同的元素发出不同的光谱,这可以用“以太扭结”的各种“振动方式”来解释。
有时候我们不得不佩服一些大师,他们虽然偶尔有点信口开河,不过极富原创力想象力。开尔文这个想法可以算是“弦论”的原生态。虽然后来化学周期表更好地被理解为原子内部结构,但开尔文列举的这几个证据都能在新兴的弦论中依稀找到一点影子。
请原谅我不能在这里具体给出任何判断两个扭结不同的方法。任何这样一个方法,都需要很多图解和文字说明。有兴趣的网友可以读姜伯驹的《绳圈的数学》或者英文书《Anintroductiontoknottheory》,作者Lickorish,属于系列GTM(graduatetextsinmathematics)175.再贴几个扭结:
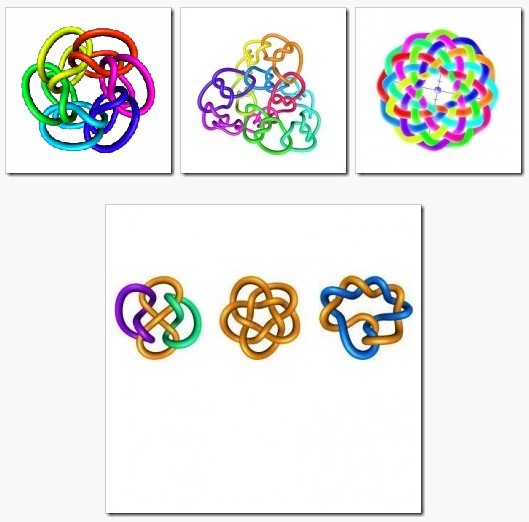
然后是一个问题:下面三个扭结中,哪两个本质上是同一种结?(来源:科学松鼠会)

