有限单群：一段百年征程

1832年的某个清晨，革命中的法国见证了又一次决斗。在某个瞬间，某位青年被对手的枪射中腹部，随后去世。在当时狂热的政治斗争中，只有寥寥数人意识到，法国，甚至世界，又失去了另一个伟大的头脑。这位青年姓伽罗华，他的最大遗产围绕着一个数学概念：群。
　　
　　在接下来的一百多年后，一群在世界各地的数学家，沿着这位青年开辟的路径，对有限群的结构进行了彻底的分析。其中的发现，可能出乎所有人的意料。
　　
　　这是一个关于群的故事，这是一个关于单群的故事。
　　
　　高度抽象的对称
　　

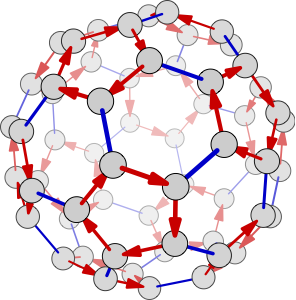
　　交错群A_5的一个Cayley图（一种群的图示）
　　
　　什么是群？一个数学家可能会给你这样的回答：
　　
　　一个群是一个集合G以及在G上的一个运算·，满足以下三个条件：
　　
　　1.存在一个G中的元素e，使得对于G中的任意元素x，有x=x·e=e·x。这样的e叫做群的单位元
　　
　　2.对于G中的任意元素x,y,z，有(x·y)·z=x·(y·z)，这是结合律
　　
　　3.对于G中的任意元素x，存在G中的一个元素y，使得e=x·y=y·x。这样的y被称为x的逆元
　　
　　这样的定义，即使是对一名刚进大学的数学系学生来说也稍显抽象。但数学的力量就在于它的抽象。它什么都不是，所以它什么都是。
　　
　　整数和加法就构成一个群。什么数加上0都不变，所以0是单位元；a+(b+c)=(a+b)+c，这是小学的加法结合律；一个数加上它的相反数是单位元0，所以相反数就是逆元。正实数和乘法也构成一个群，1是它的单位元，乘法有结合律，倒数是逆元。如果我们认为9点+5点相当于9点的5个小时后，也就是2点的话，就连时钟也构成一个群。宝石的晶体构造，电脑的压缩校验算法，以至于魔方的还原，无不牵涉“群”这个概念。而对于自然界的各种对称性，群也是对其最自然的描述方式。难怪有人会说，群就是对称，研究群，就是研究各种对称性。
　　
　　正是由于放弃了与现实的对应，像群这样的抽象数学概念才能在现实中获得广泛的对应。我们研究群，并不关心它的具体元素是什么，是x,y,z还是姬十三、猛犸、桔子都无所谓，只要知道元素通过运算产生的关系就够了，这就是群的全部。只要符合群的公理，能应用到x,y,z上的结论就能应用到姬十三、猛犸、桔子上，这就是抽象的力量。
　　
　　超越时代的孤独
　　

　　伽罗华的画像
　　
　　也正由于这种抽象，群的概念在一开始并没有很快地被接受。
　　
　　伽罗华是在研究一元五次方程的根式解时开始触及群的概念的。对于一元二次方程来说，我们可以将方程的所有解写成有关方程系数的一个根式（允许四则运算和开常数次方运算组成的式子），这称为方程的根式解。对于三次以及四次方程，也有这样的公式，可以直接从方程的系数得到方程的所有解。然而，对于五次以及更高次的方程来说，此前阿贝尔已经证明一般的公式并不存在。伽罗华要解决的，是判断何时存在这样的根式表达。
　　
　　为了解决这个问题，他首次定义了群这种代数结构，仔细地研究了群的各种性质，以及它与更高级的一种代数结构——域——的关系，并以此发展了一套理论，完整地解决了这个问题。他写下了关于这套理论与高次方程根式解的备忘录，并将其递交到法兰西科学院。
　　
　　他的不幸从此开始。
　　
　　这份备忘录的评审人是柯西。虽然认识到了伽罗华工作的重要性，柯西却没有接受这份备忘录，而是建议伽罗华修改这份备忘录以竞逐科学院的数学奖。
　　
　　伽罗华接受了这个建议，第二次提交了备忘录。
　　
　　天意弄人，评审人傅里叶之后不久就逝世了，伽罗华的

[1] [2] [3] [4] [5] 下一页