有限单群：一段百年征程

备忘录不知所踪。
　　
　　伽罗华决定最后一搏，但这也被泊松驳回，理由是“无法理解”。当消息传到伽罗华耳中时，他早已因为政治斗争而身陷囹圄，此时离他的决斗只有半年时间。
　　
　　没有人理解他的理论，或者说没有人愿意去理解他的理论。
　　
　　就是这套理论，使伽罗华的名声流芳百世。尽管他无法发表他的备忘录，但他此前发表的论文讲述了这个理论的一些基础。泊松的驳回理由，使他更认真地打磨他的理论，以冀数学界的认同。
　　
　　但死神的镰刀没有给他这个时间，上天不打算给他安排生前的荣耀。1832年5月30日，年方二十的伽罗华，迎来了他第一次也是最后一次的决斗。这场决斗的细节已经被时间之砂打磨掩盖，什么对手，什么原因，有人说是为了爱情，有人说对手背后有政治阴谋，众家各执一词。我们只知道，在这场决斗中，伽罗华腹部中枪，不久后魂归天国。
　　
　　“不要哭，阿尔弗雷德！在二十岁死去，我需要我的全部勇气。”这就是他对弟弟说的最后一句话。
　　
　　而决斗前夕给他的朋友Chevalier的信，可以算是他对世界的遗言。信中密密麻麻地写着他的数学理论，他正在思考的问题，他脑中的一切。他大概冀图某天，世界能够通过这封信，理解他。
　　
　　幸而，Chevalier实现了他挚友的意愿。伽罗华的理论，现在以他的名字命名：伽罗华理论。
　　
　　也就是这封信，吹响了一场百年战役的号角。
　　
　　构筑对称的砖块
　　

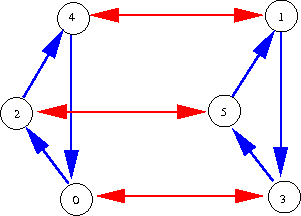
　　Z/6Z的一个Cayley图，其中可以看出它可分解为两个单群
　　
　　在伽罗华理论，乃至于更广泛的群的理论中，有一个很重要的概念：正规子群。
　　
　　我们以下只讨论那些只有有限个元素的群，它们被称为有限群。例如，魔方操作组成的群就是有限群，因为变化的可能性是有限的。而整数与加法组成的群则不是有限群，因为整数有无限个。
　　
　　在一个群里，有些元素自己会组成一个小圈子。它们并非不与外界交流，但无疑它们喜欢抱团：小圈子内的元素经过运算得到的结果仍然在这个小圈子里，而它们的逆元也在小圈子里。简而言之，这个小圈子对于原来的运算也组成一个群。这样的小圈子，叫做群的子群。
　　
　　有些子群比别的子群更特别，它们不仅自己是一个群，如果“除”原来的群，得到的也是一个群。这样的子群叫做正规子群，而它们对原来的群作“除法”得到的群叫商群。首先观察到并提出正规子群这个概念的，正是伽罗华。
　　
　　通过研究更简单的正规子群和商群，我们可以得到群的很多性质。这就是数学家特别钟爱正规子群的原因。
　　
　　如果我们将正规子群和商群看成群的一种分解的话，那么必定有着不能被继续分解的群，我们将之称为单群。
　　
　　对于任意的有限群，我们可以将其分解成一串单群，而且这样的分解是唯一的。单群在有限群论中的地位，跟素数在数论中的地位，还有原子在化学中的地位一样：它们都是构建它们所在世界的砖块。通过研究这些“砖块”，我们可以知道它们组成的各种结构的性质。如果能列出所有有限单群，就能从一个侧面了解所有离散的对称性的性质。
　　
　　有限单群就是这个故事的主角。
　　
　　与化学家当年寻找新元素的动机一样，数学家也开始了对有限单群的寻找。他们想做的跟化学家做的差不多：列一个单群的“元素周期表”。不过数学家要做的任务多了一项：证明这个“周期表”包含了所有的单群。
　　
　　这看起来不太容易，事实正是如此。
　　
　　转眼百年的长征
　　

　　Higman-Sims图，可导出散在单群Higman-Sims群
　　
　　伽罗华是寻找有

上一页 [1] [2] [3] [4] [5] 下一页