有限单群：一段百年征程

0^53个。与之相比，太阳系的原子个数也就是大约10^57个，仅仅高了两个数量级。如果我们用线性空间和矩阵变换来表示魔群的话，我们至少需要一个196883维的线性空间，才能忠实表达魔群的整体结构。这种表达方式又被称为群的线性表示。
　　
　　也正是由于魔群如此庞大，所以一开始数学家们并没有直接将它构造出来，而只能指出它的存在性。发现魔群的Griess，也要几个月后，才最终把魔群的元素个数计算出来。而魔群的直接构造，要等到9年后的1982年。那年，Griess提出了一个名为Griess代数的代数结构，而魔群恰好就是这个代数结构的自同构群。换句话说，魔群恰好刻画了Griess代数的所有对称性。值得一提的是，Griess代数的维度是196884，比196883多1。
　　
　　如果说每一族单群和每一个散在单群代表一种对称性的话，那么魔群一定有着非同寻常的对称性。体积如此庞大的群，却仍然是一个不可分解的单群，这本来就是个奇迹；而且与那些成系列的量产型单群不同，它的结构和对称性还是独一无二的。用个物理上不太恰当的比喻，如果第二大的散在单群是一颗无暇的钻石的话，按照比例，魔群大概就是一颗完全由钻石组成的星球，而且透明得能从一边看到另一边的星空。
　　
　　如果说如此瑰丽的魔群，仅仅是数学中的一个与世隔绝的孤岛的话，那数学之神未免太浪费了。
　　
　　而此时，在数学的另一个领域——数论，另一群数学家正在研究一些完全不同的东西。
　　
　　模形式理论是数论的一个分支，它研究的正是模形式。模形式是复平面上满足一定性质的函数，它们跟一类叫“椭圆曲线”的数学对象密切相关。椭圆曲线是平面上的一类曲线，它经过的整点有一种自然的群的结构，而对这些群的结构的研究可以获得整数的很多性质，包括轰动一时的费马大定理的证明。
　　
　　在模形式理论中，有一个特殊的函数占据着相当重要的地位，它叫j不变量。它的历史也不短，各种性质已经被数学家们研究得相当透彻了，也为模形式理论的发展立下过汗马功劳。它可以干净利落地展开成如下的傅立叶级数，其中每个系数都是整数：
　　

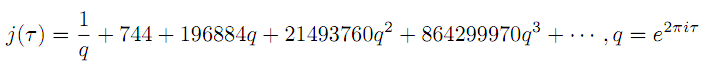
　　其中是不是有个数字很眼熟？对，就是第二个傅立叶系数196884，正好是Griess代数的维数，也就是魔群的最小忠实线性表示的维数加1。这仅仅是个巧合，还是有某种内在的联系？
　　
　　当JohnMcKay在上个世纪七十年代末将这个发现告诉Conway时（顺带一提，这位就是发明“生命游戏”的那个Conway），他们并不认为这是一个单纯的巧合。如果是3或者5这种小数字，那巧合或许还能解释，但196884的话，说是巧合未免过于牵强，“有某种尚未发现的内在联系”这个解释听起来更加合理。Conway和另一位数学家Norton随后发现，j不变量的其它傅立叶系数也与魔群的所谓不可约表示的维数有着紧密的联系：这些傅立叶系数恰好可以表示成不可约表示维数的一些简单的线性组合。这就远远不是巧合能够解释的问题了。
　　
　　在这些基础上，Conway和Norton提出了他们的所谓“魔群月光猜想”。他们猜想，存在一个基于魔群的无限维代数结构，通过魔群的不可约线性表示，它恰好给出了j不变量的所有傅立叶系数，而魔群每一个元素在这个代数结构上的作用，都自然地给出了与某个群相关的模形式。这其中牵涉到的数学，即使笔者也无从驾驭，需要长时间的学习，方能领会个中美妙滋味。
　　
　　“魔群月光”这个名字，奇怪地带着些浪漫色彩，但这不过是错觉。“月光”的原文是“moonshine”，在俚语中的意思毫不浪漫，反而是用作形容那些带点疯狂的主意。这就是当时Conway听到这个巧合之时的反应。即使对于最有想象力的数学家来说，要承认数论中被研究得相当透彻的j不变量，与有限群论这个不太相关的领域中新发现的魔群有着这么紧密的联系，这个主意也未免有些疯狂。
　　
　　但更疯狂的还在后头。
　　
　　不久，数学家们构造出了一个被称为魔群模（MonsterModule）的特殊代数结构，被认为极有可能是满足魔群月光猜想的那个代数结构。要构造这个代数结构，首先要从一个名为Leech格的代数结构开始（顺带一提，这个代数结构有着特殊的对称性，可以构造出数个散在单群），构造一个24维的

上一页 [1] [2] [3] [4] [5] 下一页