数的创生之哈密尔顿的四元数 |
|
|
| 来源:不详 更新时间:2012-9-19 16:05:28 |
|
|
|
|
看是复平面里的单位圆周,群运算就是复数的乘法。这个群通常记为U(1).它是最简单的李群。由于绝对值为1的复数乘上其它复数就相当于把相应的平面矢量旋转一个角度,所以这个群实际上等同于平面的旋转群,记为SO(2).就是说,绝对值为1的复数构成的群可以解释为实数平面(即二维实数空间)的旋转群。
让我们更真切地看看这个对应。实际上这个对应可以从复数的矩阵表示导出。从复数的乘法公式
(x+yi)(z+wi)=(xz-yw)+(xw+yz)i
可以看到,乘积的两个分量很像矩阵乘积的元素。不难猜测这个乘法可以由形如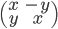 的矩阵实现。这种矩阵的主对角线对应复数的实部,副对角线对应复数的虚部。它们之间的乘法如下 的矩阵实现。这种矩阵的主对角线对应复数的实部,副对角线对应复数的虚部。它们之间的乘法如下
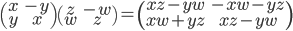
乘积矩阵的主对角线正好对应到复数乘积的实部,副对角线正好对应到复数乘积的虚部。因此,复数之间的加减乘除运算完全可以由这类形状特殊的(实数)矩阵之间的加减乘除运算来重现。
绝对值为1的复数可以表示为cosθ+isinθ,从而对应到矩阵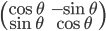 ,它恰好是二维实数平面的旋转矩阵。 ,它恰好是二维实数平面的旋转矩阵。
绝对值为1的四元数构成的群,同样也可以等同于二维复数空间的某种“旋转群”。我们类比复数的情况,来建立四元数的“复数矩阵表示”。四元数可以表示为两个复数的组合:x+yi+zj+wk=(x+yi)+(z+wi)j=α+βj.由于乘法的不交换性,βj=(z+wi)j=zj+wij=jz-jwi=j(z-wi)=jβ*.两个四元数相乘可以计算如下:
(α+βj)(γ+σj)=αγ+βjσj+βjγ+ασj=(αγ+βσ*jj+βγ*j+ασj=(αγ-βσ*)+(βγ*+ασ)j
非常类似复数的乘法公式,只是要注意额外的复共轭运算。同样不难猜测和验证,形如的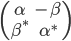 (复数)矩阵之间的乘法可以重现四元数之间的乘法。这种矩阵的主对角线对应四元数的第一个复数部分,副对角线对应四元数的第二个复数部分。 (复数)矩阵之间的乘法可以重现四元数之间的乘法。这种矩阵的主对角线对应四元数的第一个复数部分,副对角线对应四元数的第二个复数部分。
绝对值为1的四元数α+βj满足条件|α|2+|β|2=1.它们对应的矩阵因而满足条件
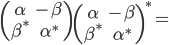
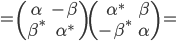
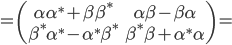
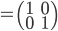
线性代数课程中,这种矩阵被称为“酉矩阵”。它是保持二维复数矢量长度的变换。它们构成一个李群,记为SU(2).我们来看几个特殊的四元数对应到哪些酉矩阵:
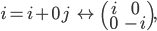
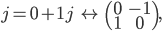
上一页 [1] [2] [3] 下一页
|
上一个数学: 有限单群:一段百年征程
下一个数学: 数学方法教你识破“神秘”巧合 |
|
|
|
|
|
|
