数的创生之哈密尔顿的四元数

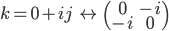
　　熟悉物理学的读者可能认出这三个矩阵很像量子力学里描述角动量的泡利矩阵。所以它们应该跟三维旋转有关系。确实，我们可以从另一个角度来看待这个绝对值为1的四元数构成的李群。这个李群在几何上是一个三维球面，它在(1,0,0,0)点的切空间是一个三维平直空间。群的元素在整个三维球面上的作用也会局部化为对这个切空间的作用。因此每个绝对值为1的四元数都可以表示为三维空间的旋转。这种表示实际上是如今四元数在数学之外的其他学科里的主要应用。
　　
　　哈密尔顿当年寻找四元数的动机本来是更简洁地描述力学和电磁学。但是后来的发展表明19世纪中叶流行起来的矢量分析更适合描述物理学。因而对四元数的研究渐渐只局限于纯数学的部分领域，成为非主流。然而，四元数的创生拓展了人们对“数”的认识，开启了对非交换的乘法结构的系统研究。发展至今，四元数成为连接诸多数学研究子领域的桥梁。
　　
　　我们知道以复数为变量的复值函数可以做微积分，形成一个理论称为“复分析”，它在纯数学、物理、工程领域都有非常重要的应用。既然四元数是复数的一种扩展，我们是否也可以建立“四元数分析”呢？显然，这里的难点在于非交换性。微积分最基本的概念“导数”是由除法定义的，而现在乘法除法都依赖于因子或除子的顺序。实践证明这是一个很本质的困难，以至于人们至今还无法建立一个令人满意的“四元数分析”理论。有兴趣、有时间、对复分析有一定了解的读者也许可以尝试一下。
　　
　　细心的读者可能会问，既然实数可以扩充到复数，复数可以扩充到四元数，那么四元数还可以继续扩充吗？答案是肯定的：数学家凯莱发现了一种“八元数”，它们之间也可以做加减乘除运算，但是乘法的性质更差了，甚至都不满足结合律，也就是说，(XY)Z≠X(YZ).然而，毕竟这样的运算存在于八维空间。更高维数呢？存在“十六元数”吗？答案是否定的：这是因为更高维的球面不具有某种几何（拓扑）性质。高维空间矢量之间乘除运算的存在性竟然跟高维球面的几何（拓扑）性质有关！这真是风马牛不相及啊。但数学就是这么不可思议。对此感兴趣的读者可以了解一下代数拓扑、矢量丛和示性类。陈省身、吴文俊等中国数学家在这些领域做出过开创性的工作。
　　
　　下篇继续介绍其他在物理学中用到的性质特异的“数”。
　　
　　附记：说到这位威廉.哈密尔顿，不能不提到他对于物理学的伟大贡献。我们可能比较熟悉20世纪初量子力学的创立留下的种种传说。其中之一是关于所谓“波粒二象性”，是说这个世界的基本组成部分既具有“粒子”的形态，又具有“波”的性质。最初的量子力学也是海森堡和薛定谔各自从“粒子”和“波”的角度创立的，分别称为“矩阵力学”和“波动力学”。之后这些量子力学的创立者们才发现，原来它们只是同一个理论的不同形态。当年海森堡和薛定谔都很自信，认为只有自己的理论才是真命天子。这种自信很可能源于他们对哈密尔顿的崇敬。海森堡的“矩阵力学”沿袭了哈密尔顿的“动力学方程”体系；薛定谔的“波动力学”则从“哈密尔顿-雅可比方程“衍生而来。两个理论都有着高贵的血统。但是他们似乎忽略了一个事实：哈密尔顿的动力学方程和“哈密尔顿-雅可比方程”本来就是等价的。如果哈密尔顿在世，他一眼就能看出矩阵力学和波动力学是同一个理论的不同表述。它们正是他本人在量子力学创立的一个世纪之前对经典力学做出的两种等价表述的升级版。实际上哈密尔顿也早就意识到了“粒子”和“光”的统一：正是他首先指出粒子动力学遵从的”最小作用量原理“和几何光学遵从的”最短光程原理“在形式上是一致的，”哈密尔顿-雅可比方程”正是解释这种统一性的关键。只不过他可能没有想到这种统一不只限于其理论表述形式的统一，而是作为物质实体的统一。我们可以猜测：如果不是四元数吸引了哈密尔顿，令其在生命的后半段全心投入该研究，他也许会更深刻地改变物理学。（来源：科学松鼠会）

上一页  [1] [2] [3]