Riemann 猜想漫谈(一)

作者：卢昌海
　　
　　我们从一则小故事开始我们的Riemann猜想之旅吧。故事大约发生在七十多年前，当时英国有一位很著名的数学家叫做GodfreyHardy(1877-1947)，在我看来他是两百年来英国数学界的一位勇者。为什么说他是勇者呢？因为在十七世纪的时候，英国数学家与欧洲大陆的数学家之间发生了一场激烈的论战。论战的主题是谁先发明了微积分。论战所涉及的核心人物一边是英国的科学泰斗IsaacNewton(1642-1727)，另一边是欧洲大陆(德国)的哲学及数学家GottfriedLeibniz(1646-1716)。这一场论战打下来，两边筋疲力尽自不待言，还大伤了和气，留下了旷日持久的后遗症。自那以后，英国的许多数学家开始排斥起来自欧洲大陆的数学进展。一场争论演变到这样的一个地步，英国数学界的集体荣誉及尊严、Newton的赫赫威名便都成了负资产，英国的数学在保守的舞步中走起了下坡路。
　　
　　这下坡路一走便是两百年。
　　
　　在这样的一个背景下，在复数理论还被一些英国数学家视为来自欧洲大陆的危险概念的时候，土生土长的英国数学家Hardy却对来自欧洲大陆(而且偏偏还是德国)、有着复变函数色彩的数学猜想——Riemann猜想——产生了浓厚的兴趣，积极地研究它，并且——如我们将在后文中介绍的——取得了令欧洲大陆数学界为之震动的成就，算得上是勇者所为。
　　
　　当时Hardy在丹麦有一位很要好的数学家朋友叫做HaraldBohr(1887-1951)，他是著名量子物理学家NielsBohr(1885-1962)的弟弟。Bohr对Riemann猜想也有浓厚的兴趣，曾与德国数学家EdmundLandau(1877-1938)一起研究Riemann猜想(他们的研究成果也将在后文中加以介绍)。Hardy很喜欢与Bohr共度暑假，一起讨论Riemann猜想。他常常要待到假期将尽才匆匆赶回英国。结果有一次当他赶到码头时，发现只剩下一条小船可以乘坐了。没办法，他只得硬着头皮登上。在汪洋大海中乘坐小船可不是闹着玩的事情，弄得好算是浪漫刺激，弄不好就得葬身鱼腹。信奉上帝的乘客们此时都忙着祈求上帝的保佑。Hardy却是一个坚决不信上帝的人，不仅不信，有一年他还把向大众证明上帝不存在列入自己的年度六大心愿之中，且排名第三(排名第一的是证明Riemann猜想)。不过在这生死攸关的时侯Hardy也没闲着，他给Bohr发去了一张简短的明信片，上面只有一句话：
　　
　　“我已经证明了Riemann猜想！”
　　
　　Hardy果真已经证明了Riemann猜想吗？当然不是。那他为什么要发这么一张明信片呢？回到英国后他向Bohr解释了原因，他说如果那次他乘坐的小船真的沉没了，那人们就只好相信他真的证明了Riemann猜想。但他知道上帝是肯定不会把这么巨大的荣誉送给他——一个坚决不信上帝的人——的，因此上帝一定不会让他的小船沉没的。[注一]
　　
　　上帝果然没舍得让Hardy的小船沉没。自那以后又过了七十几个年头，吝啬的上帝依然没有物色到一个可以承受这么大荣誉的人。
　　
　　二.Riemannζ函数与Riemann猜想
　　
　　那么这个让上帝如此吝啬的Riemann猜想究竟是一个什么样的猜想呢？在回答这个问题之前我们先得介绍一个函数：Riemannζ函数。这个函数虽然挂着Riemann的大名，其实并不是Riemann首先提出的。但Riemann虽然不是这一函数的提出者，他的工作却大大加深了人们对这一函数的理解，为其在数学与物理上的广泛应用奠定了基础。后人为了纪念Riemann的卓越贡献，就用他的名字命名了这一函数。[注二]
　　
　　那么究竟什么是Riemannζ函数呢？Riemannζ函数ζ(s)是级数表达式(n为正整数)
　　
　　ζ(s)=Σnn-s(Re(s)>1)
　　
　　在复平面上的解析延拓。之所以要对这一表达式进行解析延拓，是因为——如我们已经注明的——这一表达式只适用于复平面上s的实部Re(s)>1的区域(否则级数不收敛)。Riemann找到了这一表达式的解析延拓(当然Riemann没有使用“解析延拓”这样的现代复变函数论术语)。运用路径积分，解析延拓后的Riemannζ函数可以表示为：
　　

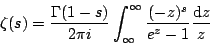[1] [2] 下一页