Riemann 猜想漫谈 (二) |
|
|
| 来源:不详 更新时间:2012-9-20 16:50:17 |
|
|
|
|
855)和法国数学家Adrien-MarieLegendre(1752-1833)。
Gauss对素数分布的研究始于1792到1793年间,那时他才十五岁。在那期间,每当“无所事事”的时候,这位早熟的天才数学家就会挑上几个长度为一千的自然数区间,计算这些区间中的素数个数,并进行比较。在做过了大量的计算和比较之后,Gauss发现素数分布的密度可以近似地用对数函数的倒数来描述,即ρ(x)~1/ln(x),这正是上面提到的素数定理的主要内容。但是Gauss并没有发表这一结果。Gauss是一位追求完美的数学家,他很少发表自己认为还不够完美的结果,而他的数学思想与灵感犹如浩瀚奔腾的江水,汹涌激荡,常常让他还没来得及将一个研究结果完美化就又展开了新课题的研究。因此Gauss一生所做的数学研究远远多过他正式发表的。但另一方面,Gauss常常会通过其它的方式——比如书信——透露自己的某些未发表的研究成果,他的这一做法给一些与他同时代的数学家带来了不小的尴尬。其中“受灾”较重的一位便是Legendre。这位法国数学家在1806年率先发表了线性拟合中的最小平方法,不料Gauss在1809出版的一部著作中提到自己曾在1794年(即比Legendre早了十二年)就发现了同样的方法,使Legendre极为不快。
有道是:不是冤家不聚首。在素数定理的提出上,可怜的Legendre又一次不幸地与数学巨匠Gauss撞到了一起。Legendre在1798年发表了自己关于素数分布的研究,这是数学史上有关素数定理最早的文献[注二]。由于Gauss没有发表自己的研究结果,Legendre便理所当然地成为了素数定理的提出者。Legendre的这个优先权一共维持了五十一年。但是到了1849年,Gauss在给德国天文学家JohannEncke(1791-1865)的一封信中提到了自己在1792至1793年间对素数分布的研究,从而把尘封了半个世纪的优先权从Legendre的口袋中勾了出来,挂到了自己那已经鼓鼓囊囊的腰包之上。
幸运的是,Gauss给Encke写信的时候Legendre已经去世十六年了,他用最无奈的方式避免了再次遭受残酷打击。
无论Gauss还是Legendre,他们对于素数分布规律的研究都是以猜测的形式提出的(Legendre的研究带有一定的推理成份,但离证明仍相距甚远)。因此确切地说,素数定理在那时还只是一个猜想,即素数猜想,我们所说的提出素数定理指的也只是提出素数猜想。素数定理的数学证明直到一个世纪之后的1896年,才由法国数学家JacquesHadamard(1865-1963)与比利时数学家CharlesdelaVallée-Poussin(1866-1962)彼此独立地给出。他们的证明与Riemann猜想有着很深的渊源,其中Hadamard的证明所出现的时机和场合还有着很大的戏剧性,这些我们将在后文中加以叙述。
【素数分布与素数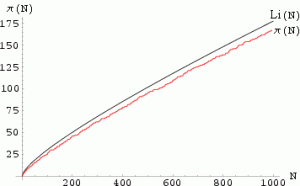 定理】 定理】
素数定理是简洁而优美的,但它对于素数分布的描述仍然是比较粗略的,它给出的只是素数分布的一个渐近形式——即小于N的素数个数在N趋于无穷时的分布形式。从有关素数分布与素数定理的图示(即右图)中我们也可以看到,π(x)与Li(x)之间是有偏差的,而且这种偏差的绝对值随着x的增加似有持续增加的趋势(所幸的是,这种偏差的增加与π(x)及Li(x)本身的增加相比仍是微不足道的——否则素数定理也就不成立了)[注三]。
那么有没有一个公式可以比素数定理更精确地描述素数的分布呢?这便是Riemann在1859年想要回答的问题。那一年是Gauss去世后的第五年,三十二岁的Riemann继德国数学家JohannDirichlet(1805-1859)之后成为了Gauss在Göttingen大学的继任者。同年的8月11日,他被选为了柏林科学院(BerlinAcademy)的通信院士(CorrespondingMember)。作为对这一崇高荣誉的回报,Riemann向柏林科学院提交了一篇论文——一篇只有短短八页的论文,标题是:论小于给定数值的素数个数。正是这篇论文将Euler乘积公式所蕴涵的信息破译得淋漓尽致,也正是这篇论文将Riemannζ函数的零点分布与素数的分布联系在了一起。
上一页 [1] [2] [3] 下一页
|
上一个数学: Riemann 猜想漫谈(一)
下一个数学: 数学模型算出书中1600多年前的“桃花源”在湖南安化 |
|
|
|
|
|
|
