四.Riemann的论文——基本思路
终于到了Riemann的论文登场的时候!如果让数学家们来评选几篇数学史上意义深远而又最为难啃的论文的话,那么我想Riemann1859年的那篇“论小于给定数值的素数个数”就算不名列榜首,起码也要挤身三甲[注一]。现在就让我们一起来领略一下那篇数学史上出名难啃的论文的主要内容。我们的叙述将采用较为现代的术语及表述方式,所用的记号将与前文保持一致——因此与Riemann的原始论文不尽相同(但主要思路是一致的),这一点要提醒有兴趣阅读Riemann原文的读者注意。
如我们在上节中所述,Euler乘积公式:
ζ(s)≡Σnn-s=Πp(1-p-s)-1
是研究素数分布规律的基础。Riemann的研究也是以这一公式作为起点的。为了消除这一公式右边的连乘积,Euler曾经对公式的两边取对数,Riemann也如法泡制(看来连乘积真是一个人人欲除之而后快的东西),从而得到:
lnζ(s)=-Σpln(1-p-s)=ΣpΣn[(1/n)p-ns]
但过了这一步,两人就分道扬镳了:Euler——如我们上节中所见——在小试身手,证明了素数有无穷多个后就鸣金收兵了;而Riemann则沿着一条布满荆棘的道路继续走了下去,走出了素数研究的一片崭新的天地。
可以证明,上面给出的lnζ(s)的表达式右边的双重求和在复平面上Re(s)>1的区域内是绝对收敛的,并且可以改写成Stieltjes积分(有兴趣的读者可自行证明):
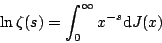
其中J(x)是一个特殊的阶梯函数,它在x=0处取值为零,以后每越过一个素数就增加1,每越过一个素数的平方就增加1/2,...,每越过一个素数的n次方就增加1/n,...。而在J(x)不连续的点(即x等于素数、素数的平方、...、素数的n次方...的点)上,其函数值则用J(x)=(1/2)[J(x-)+J(x+)]来定义。显然,这样的一个阶梯函数可以用素数分布函数π(x)表示为:
J(x)=Σn[(1/n)π(x1/n)]
对上述Stieltjes积分进行一次分部积分便可得到:
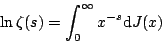
这个公式的左边是Riemannζ函数的自然对数,右边则是对J(x)——一个与素数分布函数π(x)有直接关系的函数——的积分,它可以被视为Euler乘积公式的积分形式。我们得到这一结果的方法与Riemann有所不同,Riemann发表论文时还没有Stieltjes积分——那时候荷兰数学家ThomasStieltjes(1856-1894)才三岁。
如果说传统形式下的Euler乘积公式只是Riemannζ函数与素数分布之间存在关联的朦胧征兆,那么在上述积分形式的Euler乘积公式下,这两者间的关联就已是确凿无疑并且完全定量的了。接下来首先要做的显然是从上述积分中解出J(x)来,这在当时的数学背景下并不容易,但却难不倒象Riemann这样的复变函数论大师。他解出的J(x)是(学过复变函数论的读者不妨试着证明一下):
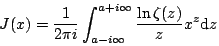
其中a为大于1的实数。上面这个积分是一个条件收敛的积分,它的确切定义是从a-ib积分到a+ib(b为正实数),然后取b→∞的极限。当Riemann写下这个公式时,只是轻描淡写地提了一句:这是完全普遍的。听上去象是在叙述一个尽人皆知的简单事实。而事实上,与Riemann所说的普遍性相匹配的完整结果直到四十年后才由芬兰数学家RobertMellin(1854-1933)所发表,现在被称为Mellin变换(MellinTransform)。象这样一种被Riemann
[1] [2] [3] 下一页
