Riemann 猜想漫谈(四)

(s)=lnξ(0)+Σρln(1-s/ρ)-lnΓ(s/2+1)+(s/2)lnπ-ln(s-1)
　　
　　对lnζ(s)作这样的分解，目的是为了计算J(x)。但是将这一分解式直接代入J(x)的积分表达式所得到的各个单项积分却并不都收敛，因此Riemann在代入之前先对J(x)作了一次分部积分，由此得到(感兴趣的读者可自行证明)：
　　

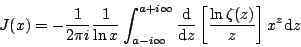
　　将lnζ(s)的分解式代入上式，各单项便可分别积出，其结果如下表所列：
　　

　　在上述结果中，对级数Σρln(1-s/ρ)的积分最为复杂，其结果-ΣIm(ρ)>0[Li(xρ)+Li(x1-ρ)]是对级数逐项积分的结果。这一结果是条件收敛的，不仅要如lnξ(s)的级数表达式中一样将ρ与1-ρ进行配对，而且还必须依照Im(ρ)从小到大的顺序求和。Riemann在给出这一结果时承认逐项积分的有效性有赖于对ξ函数的“更严格”的讨论，但他表示这是容易证明的。这一“容易证明”的结果在三十六年后的1895年被vonMangoldt所证明。另外值得指出的一点是，在Riemann对这一级数的各个单项进行积分时隐含了一个要求，那就是对所有的零点ρ，0<Re(ρ)<1[注五]，这比我们在前面提到过的0≤Re(ρ)≤1要强。这一加强看似细微(只不过是将等号排除掉而已)，其实却——如我们在后文中将会看到的——是数论中一个非同小可的结果。Riemann在文章中不仅没有对这一结果加以证明，连暗示性的说明也没有，应该被视为是他论文的一个漏洞。这一漏洞在vonMangoldt的证明中也同样存在[注六]。不过这一漏洞只是论证方法上的漏洞，是可以弥补的，论证的结果本身并不依赖于0<Re(ρ)<1这样的条件。
　　
　　由上面这些结果Riemann得到了J(x)的显形式：
　　

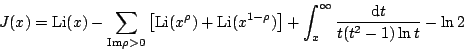
　　这一结果，连同上节给出的π(x)与J(x)的关系式：
　　
　　π(x)=Σn[μ(n)/n]J(x1/n)
　　
　　便是Riemann所得到的素数分布的完整表达式，也是他1859年论文的主要结果。Riemann的这一结果给出的是素数分布的精确表达式，它的第一项(由J(x)及π(x)的第一项共同给出)正是当时尚未得到证明的素数定理所预言的结果Li(x)。
　　
　　细心的读者可能会问：Riemann既然已经给出了素数分布的精确表达式，却没能直接证明远比该结果粗糙的素数定理，这是为什么呢？这其中的奥秘就在于Riemannζ函数的非平凡零点，在于J(x)的表达式中那些与零点有关的项，即-ΣIm(ρ)>0[Li(xρ)+Li(x1-ρ)]。在J(x)的表达式中，所有其它的项都十分简单，也比较光滑，因此素数分布的细致规律——那些细致的疏密涨落——主要就蕴涵在了这个与Riemannζ函数的非平凡零点有关的级数之中。如上所述，这个级数是条件收敛的，也就是说它的收敛有赖于参与求和的各项——即来自不同零点的贡献——之间的相互抵消。这些来自不同零点的贡献就像一首盘旋起伏的舞曲，引导着素数的细致分布。而这首舞曲的奔放程度——也就是这些贡献相互抵消的方式和程度——则决定了素数的实际分布与素数定理给出的渐近分布之间的接近程度。所有这一切都定量地取决于Riemannζ函数非平凡零点的分布。Riemann给出的素数分布的精确表达式之所以没能立即使得对素数定理的直接证明成为可能，原因正是因为当时人们对Riemannζ函数非平凡零点的分布还知道得太少(事实上当时人们所知道的也就是我们在上面已经提到过的0≤Re(ρ)≤1)，无法有效地估计那些来自零点的贡献，从而也就无法有效地估计素数定理与素数实际分布——即Riemann给出的精确表达式——之间的偏差。
　　
　　那么Riemannζ函数非平凡零点的分布对素数定理与素数实际分布之间的偏差究

上一页 [1] [2] [3] [4] 下一页