Riemann 猜想漫谈 (七)

和所付出的辛劳是怎么评价也不过分的，如我们在上节中所说，Riemann的手稿乃是诸般论题混杂、满篇公式却几乎没有半点文字说明的手稿。而且Riemann晚年的生活很不宽裕，用纸十分节约，每张稿纸的角角落落都写满了东西，使得整个手稿更显混乱。再加上Riemann所写的那些东西本身的艰深。Siegel能从中整理出如此复杂的公式对数学界实在是功不可没。为了表达对Siegel这一工作的敬意，数学家们将他从Riemann手稿中整理发现的这一公式称为Riemann-Siegel公式。Riemann若泉下有知，也当乐见他的这位后辈同胞的名字通过这一公式与自己联系在一起，因为在这之后，再也没有人会怀疑他论文背后的运算背景了。
　　
　　发表于1932年的Riemann-Siegel公式是Göttingen数学辉煌的一抹余辉。随着纳粹在德国的日益横行，大批杰出的科学家被迫或主动离开了德国，曾经是数学圣地的Göttingen一步步地走向了衰落。1933年，Landau因其“犹太式的微积分与雅里安(Aryan)的思维方式背道而驰”而被剥夺了授课资格，离开了他一生挚爱的数学讲堂。出于对战争的厌恶，Siegel也于1940年离开了德国。Göttingen的衰落是德国文化史上最深重的悲剧之一。在这场悲剧中最痛苦的也许要算是Hilbert，他是自Gauss和Riemann之后Göttingen数学传统的灵魂人物，从某种意义上讲，Göttingen也是Hilbert的灵魂。他一生为发扬Göttingen的数学传统付出了无数的心力，Göttingen记录了他一生的荣耀与自豪，而今在他年逾古稀的时候却要残酷地亲眼目睹这一切的辉煌烟消云散。1943年，Hilbert黯然离开了人世，Göttingen的一个时代走到了终点。
　　
　　十一.Riemann-Siegel公式
　　
　　Riemann-Siegel公式的推导极其复杂，不可能在这里加以介绍。不过为了使读者对Riemannζ函数非平凡零点的计算有一个大致了解，我们将对计算零点的基本思路作一个简单叙述，并给出Riemann-Siegel公式的表述(给出这一复杂公式的表述并不是为了显摆，而是因为我们将在下一节中一同来使用这一公式)。
　　
　　读者们也许还记得，在第五节中我们曾经介绍过Riemann所引进的一个辅助函数
　　
　　ξ(s)=Γ(s/2+1)(s-1)π-s/2ζ(s)
　　
　　它的零点与Riemannζ函数的非平凡零点重合。因此，我们可以通过对ξ(s)零点的计算来确定Riemannζ函数的非平凡零点。这是计算Riemannζ函数零点的基本思路。由于ξ(s)满足一个特殊的条件：ξ(s)=ξ(1-s)，运用复变函数论中的反射原理(reflectionprinciple)很容易证明(读者不妨自己试试)，在Re(s)=1/2的直线(即Riemann猜想中的临界线)上ξ(s)的取值为实数。这表明在临界线上通过研究ξ(s)的符号改变就可以确定零点的存在。这是利用ξ(s)计算零点的一个极大的优势。接下来我们将只考虑s的取值在临界线上的情形，为此令s=1/2+it(t为正实数)。利用ξ(s)的定义可以证明(请读者自行完成)：
　　
　　ξ(1/2+it)=[eRelnΓ(s/2)π-1/4(-t2-1/4)/2][eiImlnΓ(s/2)π-it/2ζ(1/2+it)]
　　
　　很明显，上式中第一个方括号内的表达式始终为负，因此在计算ξ(s)的符号改变——从而确定零点——时可以忽略。这表明要想确定Riemannζ函数的非平凡零点，实际上只需研究上式中第二个方括号内的表达式就可以了。我们用Z(t)来标记这一表达式，即：
　　
　　Z(t)=eiImlnΓ(s/2)π-it/2ζ(1/2+it)
　　
　　至此，研究Riemannζ函数的非平凡零点就归结为了研究Z(t)的零点，而后者又可以归结为研究Z(t)的符号改变。
　　
　　那么Riemann-Siegel公式是什么呢？它就是Z(t)的渐进展开式，其具体表述为：
　　

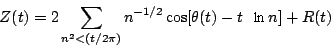
上一页 [1] [2] [3] 下一页