其中:
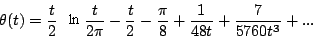
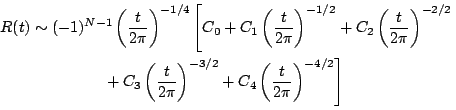
上面式子中的R(t)被称为剩余项(remainder),其中的N为(t/2π)1/2的整数部分,R(t)中各项的系数分别为:
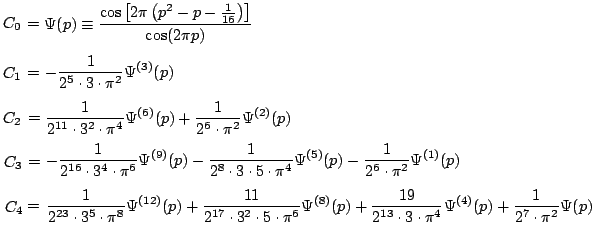
其中p为(t/2π)1/2的分数部分,Ψ(n)(p)为Ψ(p)的n阶导数。
这就是Siegel从Riemann手稿中整理出来的计算Riemannζ函数非平凡零点的公式[注四]。确切地讲它只是计算Riemannζ函数——或者更确切地讲函数Z(t)——的数值的公式,要想确定零点的位置还必须通过多次计算逐渐逼近,其工作量比单单计算Riemannζ函数的数值大得多。读者们也许会感到奇怪,如此复杂的公式加上如此迂回的步骤,在没有计算机的年代里能有多大用处?的确,计算Riemannζ函数的非平凡零点即便使用Riemann-Siegel公式也是极其繁复的工作,别的不说,只要看看C4中对Ψ(p)的导数竟高达12阶之多就足令人头疼了。但是同样一件工作,在一位只在饭后茶余瞥上几眼的过客眼里与一位对其倾注生命、不惜花费时光的数学家眼里,它的可行性是完全不同的。就像在一位普通人、甚或是一位普通数学家的眼里Riemann能做出如此深奥的数学贡献是不可思议的一样。
不过,也不要把Riemann-Siegel公式看得太过可怕,因为在下一节中,我们就将一起动手用这一公式来计算一个Riemannζ函数的非平凡零点。当然,我们会适当偷点懒,也会用用计算器,甚至还要用点计算机软件。毕竟,我们与Siegel之间又隔了大半个世纪,具备了偷懒所需的信息和工具。然后,我们将继续我们的旅途,去欣赏那些勤奋的人们所完成的工作,那才是真正的风景。
注释
1.不过在Bessel-Hagen建议Siegel研究Riemann手稿的这件事情之中,被Riemann妻子索回的那部分手稿未被提及。从这点上看,那传闻即便属实,可能也是后来的事情。
2.后来的一些数学史学家甚至认为Riemann有可能计算过多达20个零点。
3.当然这里所谓的复杂是指推导和表述上的复杂,而不是指计算零点时的复杂——后者虽然也确实复杂,却要比同等精度下的Euler-Maclaurin公式来得简单(否则就谈不上是远远胜过Euler-Maclaurin公式了)。
4.这里有两点需要提醒读者:一是Riemann手稿中C4中Ψ(p)的系数与Siegel给出的有所不同;二是我们没有使用Siegel原始论文中的记号。
二零零四年五月二日写于纽约
二零零四年五月二日发表于本站
二零一二年一月三十日最新修订
来源:科学松鼠会
上一页 [1] [2] [3]
