作者:佚名
同学们,通过“多边形”的学习我们知道,多边形是指在同一平面内由一些线段首尾顺次相接所组成的图形,连接多边形不相邻的两个顶点的线段就是多边形的对角线.可是同学们是否知道,通过画多边形及多边形的对角线还能帮助我们解决现实生活中的许多数学问题呢!
比如,学校举办足球赛,共有5个班级的足球队参加比赛,比赛采取循环制,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).
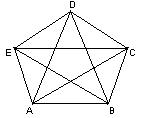
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图1可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,你们能利用多边线的对角线来解决下面的问题吗?
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,你能推算出娜娜目前已和哪几个人握了手吗?
答案:先画出6个点,A、B、C、D、E、F各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来(如图所示).
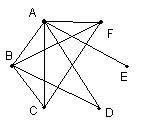
先看姣姣(A)和红红(E).姣姣已握手5次,说明姣姣与另外5人都握了手,因此代表姣姣的A点与B、C、D、E、F这5点都有一条线段连接;红红握手1次,他只能是与姣姣握的手了,所以E点只能与A点之间有线段连接,与其它各点再也不能有线段连接了.
其次分析林林(B).林林已握手4次,由于他没有可能与红红握过手,所以只能是与剩下的四个人姣姣、可可、飞飞和娜娜握过手了,因此,点B与A、C、D、F四点之间有线段连接.
再看飞飞(D).飞飞已握手2次,而代表飞飞的D点已与A、B两点有线段连接了,所以D点与其它的点不能再有线段连接了.
最后考察可可(C).可可与3人握了手,但已不能是与飞飞和红红握的手了,所以代表可可的点C只能与A、B、F三点有线段连接.
现在观察图形,与代表娜娜的点连接的线段有3条(AF、BF和CF),这说明姣姣、林林和可可三人已与娜娜握过手.(来源:凤凰数学)
