学过微积分的朋友都知道,二阶导数是一个非常重要的概念。一般来讲,二阶导数可以拿来判定一个函数的极值点以及函数在某个区间的凹凸性:
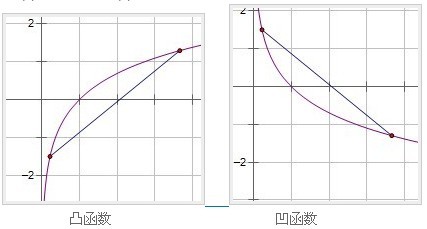
若f(x)的二阶导数f''(x)>0,函数是凹函数,反之就是下凸函数。
并且函数的凹凸性还和其极值相关:
若f''(x)>0,则函数在相应的区间有最大值;
若f''(x)<0,则函数在相应的区间有最小值。
这里要说明的是,国内的很多书(包括同济版的教材),所讲的凹凸性与国际上的凹凸性是恰恰相反的,也就是说,如果你读国外的书,上面的凹函数就是高等数学教材的凸函数,而凸函数就是凹函数。也希望教育部能够出来统一统一。
当然上面都不是这篇文章的重点,如果只是这样介绍的话也太没有意思了,我在无聊中(是一天无聊看到我头像想到的)想到一个有意思的办法来表示这个东西,那就是下面的表情图,这个只限于国内的教材,国外就是刚好相反。
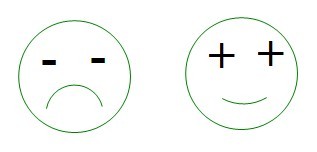
左边的图,眼睛是负号,表示二阶导数小于零,嘴巴上弯,表示这是一个凸函数,右边的图也是如此。这个图刚好说明了二阶导数负号与函数图象凹凸性之间的关系,我觉得是惟妙惟肖,不知道各位如何,哈哈,权当一乐。(来源:学夫子数学博客)
|
