作者:佚名
黄金斐氏数列,我在前面的文章中已经介绍过,也就是下面的数列
1,γ,γ2,γ3,γ4,γ5,γ6,……,γk,γk+1,……
其中γ=1.618……,也就是著名的黄金分割比,通常我们用δ表示另外一个黄金分割比0.618……,即:
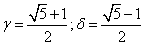
正如大家所看到的,这个数列既是斐氏数列,又是等比数列,除了在上面的数列中每一项乘以一个常数以外,这是唯一满足既是斐氏数列又是等比数列的数列。所以等比数列满足的性质在这里也满足。
一般的斐氏数列,后一项与前一项的比值是交叉地接近γ,而这个数列永远都是等于γ。在斐氏数列F(0,1),即首项为0和1的数列中,具有下面的性质:
(Fn)2=Fn-1Fn+1±1
也就是任意一项的平方与前后两项的乘积有1的偏差,在其他斐氏数列中都有一定的偏差,这刚好造就了著名的一道数学谜题的形成。但是在黄金斐氏数列中,就没有偏差,我想大家都能够看出来,因为这恰好是等比数列的一个性质。由此你也看出等比数列与斐氏数列的关系所在,等比数列满足:
(Fn)2=Fn-1Fn+1
黄金斐氏数列就是连接这两种数列的纽带。
另外一个方面,任意一个斐氏数列,如果你从首项开始,继续往另一个方向写,几乎都会出现负数的吧!比如:
以6和4开始,按照相反的方向书写其数列:6,4,2,2,0,2,-2,4,-6,……从后面往前看就是一个斐氏数列。再则从1.618和1开始写:1.618,1,0.618,0.382,0.236,0.146,0.090,0.056,0.034,0022,0.012,0.010,0.002,0.008,-0.006,……
但是黄金斐氏数列是个例外,他永远也不会出现负数。如果你继续写下去,其数列就会变成下面的:|
……,δk+1,δk,……,δ6,δ5,δ4,δ3,δ2,δ,1,γ,γ2,γ3,γ4,γ5,γ6,……,γk,γk+1,……
所以他永远都不会出现负数,尽管越来越接近于负数。说白了这也是等比数列所造就。下面我们将证明,满足这个条件的数列也非黄金斐氏数列莫属。实际上我们可以证明的,这个性质的证明过程也是充满意义。
证明黄金斐氏数列的独一无二
证明:假设最开始的两个数为a,b,a>b>0,我们反写出这个数列,即用前一个数减去后一个数得到新数:
a,b,a-b,2b-a,2a-3b,5b-3a,5a-8b,13b-8a,13a-21b,……
你是否觉得其中出现的系数和斐波那契数列有些关系?是的,实际上,我们可以推出所有斐氏数列的通项公式,如果记斐氏数列为:F1=0,F2=1,Fn+2=Fn+1+Fn。并设上面的数列的项从左到右为Qn,那么有:
将斐波那契数列写在这里,以便和下面的公式对照。0,1,1,2,3,5,8,13,21
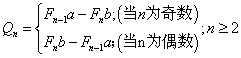
这个式子其实蕴含着所有斐波那契数列的通项公式,不过今天先不管这个,我们先用它来证明我们的结论:若斐氏数列中没有负数项,则其必为黄金斐氏数列,或者是黄金斐氏数列乘以一个常数。
按照要求,必须满足对于所有的n,Qn>0.
①:当n为奇数时:
Fn-1a-Fnb>0,即:
a/b>Fn/Fn-1
而根据斐波那契数列的性质,当n为奇数的时候,Fn/Fn-1的值是越[1] [2] 下一页
|
