作者:学夫子
前不久我们在《欧氏对局》的两篇文章里介绍了欧氏对局,任意给定两个不相等的数m和n,且n>m采用欧氏对局的规则,将有下面的结论
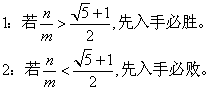
我们的欧氏对局限制在自然数的范围,将会有上面的结果,我们惊奇地发现,决定欧氏对局的,竟然是黄金分割比!详细可以参考相关文章。如果我们今天将思路扩展一下,最先的数不限制在自然数,而是一切实数的话,结果会怎样?
我们要注意的是,对于任意的两个实数,按照欧氏对局的规则不一定就会出现零,比如
π,3,π-3,6-π,9-2π,5π-12,……
但是也有可能出现零,比如1.5和2.3
2.3,1.5,0.8,0.7,0.1,0.6,0.5,0.4,0.1,0.3,0.2,0.1,0.1,0
再比如1/3和1/5
1/3,1/5,2/15,1/15,1/15,0
实际上我们可以看到,如果n和m都是有理数的话,最终会出现零,因为将两个有理数化为同分母的分数以后,最终相减的只是分子在相减,实际上也就相当于两个自然数的情况。但是若两个数是无理数,也有可能出现零,比如√2和2√2,最终就会出现零。假设最终出现的是0和a,其中a为实数,反推回去就会知道,不可能出现无理数,也就是无理数的最终结果一定是无理数。如果a为无理数,则最初的数对只可能是(ka,ha)其中k和h均为整数的形式,换句话说,只要n/m是一个有理数,那最终结果就可以分出胜负。那么这种情况下的胜负情况又是如何?是否和自然数的胜负情况一样的呢?
1:假设n和m均为有理数,将他们化成同分母的分数m=g/p,n=h/p。我们可以看到,最终的操作其实只是在分子上进行,所以结果的胜败也就是等同于g和h,而g/h=m/n,所以我们可以看到,这种情况仍然满足结论。
2:如果n和m都是无理数,并且n/m是有理数,那么可以令n=pa,m=qa,其中a为一个无理数,所以实际上后面的进行过程都只是在p和q之间进行,因为a一直都被带着走,而p/q=n/m,所以可以说在这种情况下,仍然满足欧氏对局的结论。
实际上上面所有的讨论过程可以归结为:数对(m,n)的胜败与(am,an)的胜败是一样的,因为每一步你都可以把公因式带着走。这也符合我们的结论,即胜败只取决于这两个数的比值。以一个例子说明吧:
(1/3a,0.5a)=(2/6a,3/6a)→(2/6a,1/6a)→(1/6a,1/6a)→(0,1/6a)
大家可以看到,实际上整个过程就是数对(1,2)的对局过程,而对于1/6a至始至终都跟着走的。不管a是整数有理数还是实数,甚至于是一个多项式,都是一样的道理,所以对于实数对(n,m)的欧氏对局,我们依然有下面的结论:
1:若n/m不是有理数,则这样的欧氏对局不可能会有结果。
2:若n=m,则先手为胜。
3:若n≠m,n>m,且n/m为有理数,则:
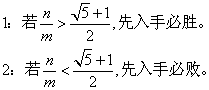
来源:学夫子数学博客
|
