Riemann 猜想漫谈(八)

这两部分(即主项及剩余项中的第一项)可得:
　　
　　Z(14.1)≈-0.342160+0.312671=-0.029489
　　
　　类似地，对于t=14.2，(t/2π)1/2≈1.503330，θ(t)≈-1.702141。因而主项2cos[θ(t)]≈-0.261934，剩余项R(t)中p≈0.503330，从而其中第一项(即C0项)为C0(t/2π)-1/4≈0.312129。由这两部分(即主项及剩余项中的第一项)可得:
　　
　　Z(14.2)≈-0.261934+0.312129=0.050195
　　
　　显然，如我们所期望的，Z(14.1)与Z(14.2)的符号相反，这表明在t=14.1与t=14.2之间存在Riemannζ函数的非平凡零点。当然，我们还没有考虑C1~C4项。这些项中带有C0的各阶导数，计算起来工作量非同小可，有违休闲的目的，因此就只好偷点懒了。熟悉计算软件的读者可以动用Maple、Matlab或Mathematica之类的计算软件来算一下。对于其他读者来说，我们就把算得的结果直接列在下表中了(其中包括我们手工算得的结果)：
　　

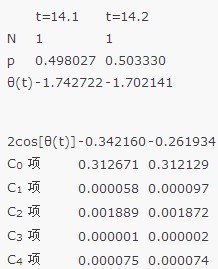
　　Z(t)-0.0274460.052042
　　
　　从表格所列的结果中可以看到，剩余项中的高阶项的贡献虽然有所起伏，但与第一项相比在总体上是很小的。对我们来说，这当然是很令人欣慰的结果，因为它表明我们手工所能计算的部分给出的贡献是主要的。这还是t较小的情况，随着t的增加，由于高阶项中所含t的负幂次较高，其贡献会变得越来越小[注二]。不过要严格表述这种趋势并予以证明，却绝非轻而易举。事实上Riemann-Siegel公式作为Z(t)的渐进展开式，其敛散性质与误差估计都是相当复杂的。
　　
　　现在我们知道了Riemannζ函数在t=14.1与t=14.2之间存在零点。如果我们再仔细点，注意到Z(14.1)与Z(14.2)距离Z(t)=0的远近之比为0.027446:0.052042，用线性内插法可以推测零点的位置为：
　　
　　t≈14.1+(14.2-14.1)×0.027446/(0.027446+0.052042)≈14.1345。
　　
　　这与现代数值t=14.1347的相对偏差只有不到十万分之二！即使只估计到C0项(这是我们自己动手所及的范围)，其误差也只有不到万分之二(请读者自行完成内插法计算并验证误差)。
　　
　　好了，猎物在手，我们的简短休闲也该见好就收了。大家是否体验到了一些成就感呢？要知道，Riemannζ函数的零点可是在Riemann的论文发表之后隔了四十四年才有人公布计算结果的哦。当然，我们用了Riemann-Siegel公式，但这没什么，一个好汉三个帮嘛！再说了，DIY哪有真的百分之百从头做起，连工具设备都包括在内的？想象一下，如果你DIY出来的陶器能够把缺陷控制在万分之二以内，那是何等的风光？当然，倘若你可以退回一百多年，把这个结果抢在Gram之前公布一下，那就更风光了。
　　
　　在本节的最后，还有一件可能让大家有成就感的事情要提一下。那就是我们所用的估计零点的方法——即从使2cos[θ(t)]为零的点出发，然后依据R(t)的数值对其进行修正[注三]，最后再用Z(t)的符号变化来确定零点的存在——暗示着Riemannζ函数在临界线上的零点数目大致与cos[θ(t)]的零点数目相当。而后者大约有(请大家DIY)θ(t)/π~(t/2π)ln(t/2π)-(t/2π)个。不知大家是否还记得，这正是我们在第五节中介绍过的Riemann那三个命题中迄今无人能够证明的第二个命题！当然，我们这个也不是证明(真可惜，否则的话，嘿嘿……)，但这应该使大家对我们的休闲手段之高明有所认识吧？
　　
　　注释
　　
　　1.要注意的是，Z(t)在一个区间的两端具有不同符号只是Riemannζ函数在该区间内存在零点的充分条件，而非必要条件。换句话说，假如我们不幸发现Z(t)在我们所取的两点上具有相同的符号，我们并不能由此直接得出结论说Riemannζ函数在这两点之间不存在零点。至于这是为什么，请大家DIY。

上一页 [1] [2] [3] 下一页