Riemann 猜想漫谈 (十)

ng)。ZetaGrid刚启动的时候，加入系统的计算机只有10台，半年后就增加到了500台，这些都是IBM实验室的内部计算机。一年后，Wedeniwski将ZetaGrid推向了互联网，任何人只要下载安装一个小小的软件包就可以使自己的机器加入ZetaGrid，此举很快吸引了大量的参与者。很快地，在ZetaGrid上的联网计算机总数就稳定在了一万以上。虽然ZetaGrid上的多数计算是利用那些联网计算机的闲散CPU时间进行的，但涓涓小溪可以汇成浩瀚江海，由如此大量的计算机所形成的总体运算能力依然十分可观。到了2004年8月，即ZetaGrid诞生三周年的日子，这一系统所计算的零点总数已超过了八千五百亿个(其中有六百万个是由本文作者的计算机贡献的)，而且还在以大约每天十亿个以上的速度增加着[注二]。
　　
　　十六.零点的统计关联
　　
　　除了不计算具体数值这一特点外，前面所介绍的那些大规模零点计算还有一个特点，那就是都只针对前N个零点。换句话说，所有那些计算都是以第一个零点为起始的。它们所验证都只是复平面上0<Im(ρ)<T这一区间内的零点。除了这类计算外，在零点计算中还有一类计算也十分重要，那就是针对一个虚部很大的区间T1<Im(ρ)<T2的计算(即从某个很大的序号开始的零点计算)。这类计算中最著名的人物是出生于波兰的数学家AndrewOdlyzko(1949-)，他在二十世纪八十年代末和九十年代初对序号在1020-30,769,710和1020+144,818,015之间的总计175,587,726个零点进行了计算。2001年和2002年，他更是把计算的起始点推进到了第1022和1023个零点附近，所计算的零点数目也分别增加到了一百亿和两百亿个。Odlyzko的这些计算不仅所涉及的区域远远超出了包括ZetaGrid在内的所有其它零点计算的验证范围，而且还包含了对零点数值的计算。这些计算对于研究Riemann猜想的意义不仅在于它们提供了有关这一猜想的新的数值证据，更重要的是它们为一类新的研究，即研究Riemannζ函数的非平凡零点在临界线上的统计关联提供了数据。这也正是Odlyzko进行这类计算的目的。
　　
　　Odlyzko为什么会想到要为研究零点的统计关联提供数据呢？这还得从二十世纪七十年代初说起。当时英国Cambridge大学(剑桥大学)有位来自美国的研究生叫做HughMontgomery，他所研究的课题是零点在临界线上的统计关联。
　　
　　Montgomery这个名字不知大家有没有觉得面熟？对了，本系列每一篇文章所引的共同题记正是出自此人！
　　
　　我们以前谈论零点分布的时候，所关心的往往只是零点是否分布在临界线上。Montgomery的研究比这更进一步。他想知道的是，假如Riemann猜想成立，即所有非平凡零点都分布在临界线上，那它们在临界线上的具体分布会是什么样的？
　　
　　在Montgomery进行研究的时候虽然已经有Rosser对前三百五十万个零点的计算结果(参阅第十三节)，但如我们在上文中所说，那些计算并不涉及零点的具体数值，从而无法为他提供统计研究的依据。因此Montgomery只能另辟蹊径，从纯理论的角度来研究零点在临界线上的统计关联。
　　
　　Montgomery对零点分布的这一理论研究从某种意义上讲恰好与Riemann对素数分布的研究互逆。Riemann的研究是着眼于通过零点分布来表示素数分布(参阅第五节)，而Montgomery的研究则是逆用Riemann的结果，着眼于通过素数分布来反推零点分布。
　　
　　不幸的是，素数分布本身在很大程度上就是一个谜(否则Riemann也就不会试图通过零点分布来研究素数分布了)。除了素数定理外，有关素数分布的很多命题都只是猜测。而素数定理，如我们在第七节中看到的，与零点分布的相关性非常弱，不足以反推出Montgomery感兴趣的信息。于是Montgomery把目光投注到了比素数定理更强的一个命题，那便是Hardy与Littlewood于1923年提出的关于孪生素数(twinprime)分布规律的猜测，即迄今尚未被证明的著名的强孪生素数猜想[注三]。Montgomery以Riemann猜想的成立为前提，以Riemann的公式及Hardy与Littlewood所猜测的孪生素数分布规律为依据，研究提出了一个有关Riemannζ函数的非平凡零点在临界线上的分布规律的重要命题：
　　

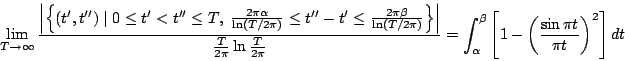上一页 [1] [2] [3] [4] 下一页