Riemann 猜想漫谈 (十)

　　上式中t'和t''分别表示一对零点的虚部，α和β是两个常数(α<β)。很明显，上式表示的是零点的对关联(paircorrelation)规律。这一规律被称为Montgomery对关联假设(Montgomerypaircorrelationconjecture)，其中的密度函数ρ(t)=1-[sin(πt)/πt]2则被称为零点的对关联函数(paircorrelationfunction)。
　　

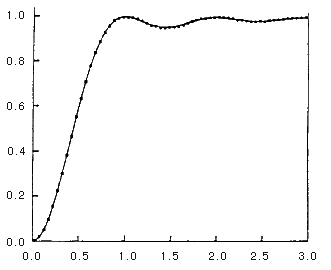
　　【零点的对关联函数】
　　
　　从上述分布规律中可以看到limt→0ρ(t)=0，这表明两个零点互相靠近的几率很小。换句话说Riemannζ函数的非平凡零点有一种互相排斥的趋势。这一点很有些出乎Montgomery的意料。Montgomery曾经以为零点的分布是高度随机的，如果那样的话，对关联函数应该接近于ρ(t)≡1。这一分布也不同于Montgomery当时见过的任何其它统计分布——比如Poisson分布或正态分布——中的对关联函数，它与素数本身的分布也大相径庭。
　　
　　这一分布究竟有何深意呢？对Montgomery来说还是一个谜。
　　
　　大家也许还记得，在第五节中我们曾经介绍过Riemann提出的三个命题，其中第一个命题(也是迄今唯一被证明的一个)表明在区间0<Im(ρ)<T内Riemannζ函数的非平凡零点的数目大约为(T/2π)ln(T/2π)-(T/2π)。由此不难推知(请读者自行证明)Riemannζ函数相邻零点的间距(即虚部之差)平均而言大约为Δt~2π/ln(t/2π)。这一间距随t而变，这使得Montgomery对关联假设的形式呈现出一点表观上的复杂性。有鉴于此，Montgomery之后的数学家(比如Odlyzko)对零点的虚部做了一点处理，引进了间距归一化的零点虚部：
　　
　　n=(t/2π)ln(t/2π)
　　
　　利用这一定义，相邻零点的平均间距被归一化为了Δn~1，而Montgomery对关联假设则可以简化为(请读者自行证明)：
　　

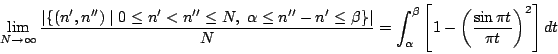
　　Montgomery对关联假设提出之后，一个很自然的问题就是：零点分布果真符合这一假设吗？这正是Odlyzko登场的地方。由于Montgomery对关联假设涉及的是对关联在T→∞情形下的渐进分布，因此要想对这一假设进行高精度的统计检验，最有效的办法是研究虚部很大的零点的分布，这也正是Odlyzko将零点计算推进到1020及更高的区域，并且计算其数值的原因。那么这两人的研究结果的匹配程度如何呢？我们在右上方的图中给出了Montgomery零点对关联假设中的关联函数(曲线)及由Odlyzko利用1020附近七千万个零点对之进行统计检验的结果(数据点)。
　　
　　两者的吻合几乎达到了完美的境界。
　　
　　1972年春天，刚刚完成上述零点统计关联研究的Montgomery带着他的研究成果飞往美国圣路易斯(St.Louis)参加一个解析数论会议。在正式行程之外，他顺道在Princeton高等研究院(InstituteforAdvancedStudy)做了短暂的停留。没想到这一停留却在数学与物理之间造就了一次奇异的交汇，我们Riemann猜想之旅也因此多了一道神奇瑰丽的景致。
　　
　　注释
　　
　　1.举个例子来说，虽然早在1982年teRiele就“计算了”前三亿个零点，但直到1985年Odlyzko与teRiele才合伙对区区两千个零点做了真正的数值计算(精度达小数点后一百位)，并以此为基础一举否证了Mertens猜想(参阅第六节的注释)
　　
　　2.可惜的是，看似如日中天的ZetaGrid在那之后不久就迎来自己的结局，而且是一个不太走运的结局。关于这个结局

上一页 [1] [2] [3] [4] 下一页