将乘法转化为加减

作者：学夫子
　　
　　自从人类发明乘法运算以来，大概就已经认识到了乘法的复杂和加减的简便，于是在很多时候，将乘法运算转化为加减运算便成为计算数学的一大研究课题了。姑且不谈这一问题的历史，今天就举一些在中学数学中出现的“将乘法转化为加减法”的例子。
　　
　　乘法法则：
　　
　　这种方法是基于下面一个公式：
　　

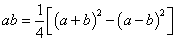
　　这个公式应该是最早的将乘法运算转化为加减运算的方法了。但这个方法的缺点是显而易见的，因为我们最终还是要计算平方，我相信对于某些数，计算其平方并不比计算一般的乘法简单。这时候三角函数的发展提供了另外一种方法。
　　
　　三角公式：
　　
　　2cosxcosy=cos(x+y)+cos(x-y)
　　
　　此公式最早由阿拉伯的尤努斯提出，在对数出现以前，这个式子替代了乘法公式而成为乘法转化为加减法运算的最好工具。方法很简单，那时候关于三角学最有用的工具就是三角函数表，这种表最早来源于印度，在阿拉伯人手里得到发扬光大。比如要计算2.3×3.4，先计算出0.23×0.34，利用三角函数表查出0.23所对应的角度76.7°和0.34所对应的角度70.1度，那么2×0.23×0.34≈cos(76.7+70.1)+cos(76.7-70.1)≈-0.83701322+0.99341322=0.1564,进而0.23*0.34≈0.0782，那么2.3*2.4≈7.82这与真实结果很非常接近（此处巧合刚好相等）。将复杂的乘法运算转化为经过简单的查表运动，这肯定大受欢迎。
　　
　　当然，除了这一个公式，其他的三个积化和差公式一样可以达到这一目的。
　　
　　对数：
　　
　　这是最有效的工具之一。并且当对数于康熙时期传入中国的时候，其最初的作用也正是如此——将乘除法运算转化为加减运算。相信大家都知道这里采用的公式就是:
　　

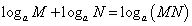
　　那时候一个重要的工具，就是一张“对数表”，以2为底（或者以10为底），将真数和借数（对数值）成对列成表格，故称“对数”。比如还是要计算2.3*3.4，从对数表里面查出2.3和3.4所对应的对数值为0.361727836和0.531478917，于是log(2.3*3.4)=0.8932067531,再利用对数表即可查出2.3*3.4的近似值为7.82（实际上就是10的0.8932067531次方）。对数的优势是显而易见的，因为他可以直接计算除法，而无须把除法转化为乘法。
　　
　　除此之外，在高等数学里还有非常类似的方法，不过这都远不是中学数学的范围。中学数学学过的函数类型无非就是那么几种，对数函数和三角函数在这里都用上了。如果把乘法的概念进行推广，而不仅仅是局限于实数的乘法，那么概率论、集合论里的某些运算都有这样的思想。不过这与实数运算的关系不明显，在这里就不提了。（来源：学夫子数学博客）