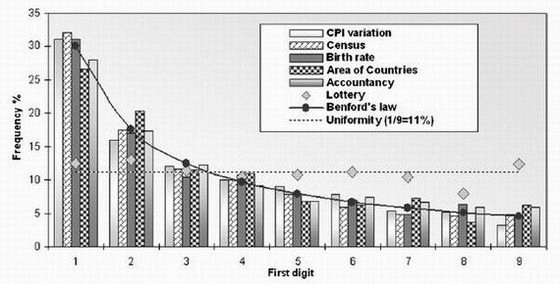
本图表中的几个数据范例来自于西班牙国家统计局,数据是按照本福特对数定律统计的。然而,按照彩票获得的数据是随机的和统一的。
您住宅地址号码是以a1开始的吗?根据一个奇特的数学定律统计,约三分之一的住宅号码是以1作为其首个数字的。其它许多几乎没有任何共通性的地区也有相同的情况:比如道琼斯指数的历史数据、个人电脑中文件储存的大小排列顺序、世界主要河流的长度、报纸头版头条的数字及其它许多事情。
该定律根据其第二位奠基人弗兰克·本福特的名字被命名为本福特定律。通用电气公司物理学家本福特于1935年发现了这一定律。该定律告诉人们在各种各样不同数据库中每个数字(从1到9)作为首个重要阿拉伯数字的频率。
除数字1始终占据约三分之一的出现频率外,数字2的出现频率为17.6%,3出现的频率为12.5%,依次递减,9的出现频率是4.6%。在数学术语中,这一对数定律的公式为F(d)=log[1+(1/d)],此公式中F代表频率,D代表待求证数字。
这一现象让人觉得很奇怪,来自科尔多瓦大学的科学家杰赫斯·托里斯、桑索利斯·费尔罗德滋、安东尼奥·迦米洛和安东尼奥·索拉同样也如此认为。科学家们在《欧洲物理杂志》上发表了一篇题为“数字如何开始?(第一数字定律)”的文章,该文章对这一定律进行了简要的历史回顾。他们的论文同时还对第一数字定律的有效应用进行了阐述,并对为何没有人能够对这一数字出现频率现象做出合理解释的原因进行了阐述。
等离子体物理学专家托里斯说,“自从我了解本福特定律以来,它一直是我很感兴趣的问题之一。在统计物理学课堂上,我一直将此定律作为一个令人惊奇的范例来激发学生们的好奇心。”托里斯解释道,在本福特之前,有一位深受尊敬的天文学家名为西蒙·纽库姆,他在1881年发现了这一定律。纽库姆同时代的科学家们并没有对他的科学发现引起足够重视。本福特和纽库姆两位科学家均对这一定律感到困惑:当浏览对数表书籍时,他们注意到书的开始部分要比结束部分脏得多。这就是说他们的同事到图书馆后,选择各种各样学科书籍时首选第一页开始阅读。
本福特对此疑问的观察要比纽库姆更深入一些。他开始对其它数字进行调查,发现各个完全不相同的数据,比如人口、死亡率、物理和化学常数、棒球统计表、半衰期放射性同位数、物理书中的答案、素数数字和斐波纳契数列数字中均有“第一数字定律”现象的出现。换句话说就是只要是由度量单位制获得的数据都符合这一定律。
另一方面,任意获得的和受限数据通常都不符合本福特定律。比如,彩票数字、电话号码、汽油价格、日期和一组人的体重或者身高数据是比较随意的,或者是任意指定的,并不是由度量单位制获得的。
正如托里斯和他的同事所解释的,数十年来科学家紧随本福特对这一数字现象进行研究,但是除了发现更多的例子外,他们几乎没有发现有关比第一数字定律本身更多的东西。然而科学家们还是发现一些奇特现象。比如当对数据库中的第二重要数字进行调查时,该定律仍然发挥着作用,但是第二重要数字的重要性却降低。同样,第三和第四重要数字所展现出来的特征就开始变得相同起来,第五重要数字的频率为10%,刚好是平均数。第二个奇特现象引发了更多的科学兴趣:
科学家们在他们所发表的文章中写到,“1961年,皮克汉姆发现了首个常规相关结论,该结论显示本福特定律是一个尺度不变原理,同时也是唯一一个提出数字尺度不变原理的定律。那就是说,由于是以公里来表示世界河流的长度,因此它满足本福特定律,同样以英里、光年、微米或者其它长度单位数字都会满足这一定律。”
托里斯同时还解释到,在二十世纪晚期,一些重要的预测理论(基数恒定性及唯一性等)被特德.希尔和其它数学家证实。虽然一些范例(比如住宅地址号几乎总是以数字1开头,低位数总是出现在高位数之前)得到了解释,但是目前仍然没有找到任何能解释各种范例的能用判断标准。科学家们同时还解释到,没有任何优先标准能够告诉我们什么时候应当或者不应当遵守这一定律设置数字。托里斯说,“现在对该定律的研究取得了许多理论成果,但是一
[1] [2] 下一页
