Riemann 猜想漫谈 (十五)

的工作。在Selberg落户高等研究院二十几年后的一天，部分地正是因为这种担心，让年轻的Montgomery踏上了Princeton之旅，从而有了我们在第十七节中叙述过的那个数学与物理交汇的动人故事。
　　
　　二十六.临界线定理
　　
　　对于我们这个系列来说，在Selberg的工作中最重要的，显然是他在Riemann猜想研究上的成就。如前所述，他的这一研究是在二战期间进行的。出于对Ramanujan的兴趣，Selberg对剑桥大学的“三剑客”——即Ramanujan、Hardy、Littlewood——的工作进行了深入研究。这其中Hardy与Littlewood所证明的有关Riemannζ函数非平凡零点分布的Hardy-Littlewood定理引起了他的极大兴趣。Hardy-Littlewood定理是一个非常漂亮的定理，但它的结果却太弱，因为——如我们在第二十四节中所介绍的——它所能确立的位于临界线上的零点数目相对于非平凡零点的总数来说，其渐近比例等于零。
　　
　　Selberg想要做的是改进这一结果。
　　
　　Hardy与Littlewood都是英国顶尖的数学家，虽然他们的结果距离解决Riemann猜想还非常遥远，但他们这项工作思虑周详、推理严谨，几乎没有留下任何空隙能让别人去填补。或者换句话说，他们在这项工作中所采用的方法已经被推到了极致。这一点Hardy与Littlewood自己也很清楚，在论文中他们明确表示用这一方法已经难以取得进一步的结果了。
　　
　　因此，要想改进Hardy与Littlewood的结果，就必须突破他们所用的方法。我们知道(详见第二十三、二十四节)，在Hardy与Littlewood所用的方法中一个很关键的部分，就是对2ξ(z)xz-1/z(z-1)的积分进行研究。Hardy最初研究的是2ξ(z)xz-1/z(z-1)在无穷区间(1/2-i∞,1/2+i∞)上的积分，而在Hardy与Littlewood的合作研究中，为了得到临界线上零点分布的细致结果，这一积分范围被细化成了临界线上的任意有限区间(s-ik,s+ik)，其中Re(s)=1/2。从选择积分区间的角度讲，这一推广已经达到了极致。
　　
　　那么想要突破Hardy与Littlewood的方法，该从哪里下手呢？Selberg把目光盯在了被积函数上。Selberg发现，如果我们用一个适当的函数对Hardy与Littlewood所用的被积函数2ξ(z)xz-1/z(z-1)进行“调制”，就有可能使对其积分的研究变得更为精准。为此他把自己的注意力放在一个更普遍的积分：

　　
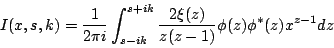
　　上。这个积分与Hardy与Littlewood所用的积分相比多了一个被积因子φ(z)φ*(z)，这个因子就是Selberg引进的调制函数，也是他在方法上的突破。
　　
　　那么什么样的调制函数比较有利于对这个积分进行研究呢？Selberg认为应该选一个能够对ξ(z)在零点附近的行为进行某种控制的函数。这种函数的一个比较容易想到的选择是φ(z)=[ζ(z)]-1/2。由于ζ(z)与ξ(z)具有同样的零点，因此用这个调制函数可以完全消去ξ(z)的零点。但这个选择有一个不利之处，那就是它在z=1处具有奇异性。为了避免这一奇异性对φ(z)的解析延拓造成麻烦，Selberg对[ζ(z)]-1/2的展开式[ζ(z)]-1/2=Σnαnn-z进行了截断处理，他引进了一个新的级数φ(z)=Σnβnn-z。这个新级数的系数βn在n≤N(N为某个很大的正整数)时取为[1-ln(n)/ln(N)]αn，而在n>N时则取为零。这样引进的φ(z)是一个至多只有N+1项的有限级数，从而对所有的z都解析。另一方面，在N很大时它是对[ζ(z)]-1/2的近似，因此通过对N进行调节，Selberg可以对ξ(z)在零点附近的行为进行某种控制。
　　
　　这一调制函数果然不负厚望，通过它的辅助，Selberg经过复杂的计算与推理，终于证明了一个比Hardy-Littlewood定理强得多的结果。这个结果被称为临界线定理(criticallinetheorem)[注四]：
　　

上一页 [1] [2] [3] 下一页