Riemann 猜想漫谈 (十四)

作者：卢昌海
　　
　　在Bohr与Landau研究零点分布的同时，另一位为Riemann猜想而着迷的数学家——Hardy——也没闲着。1914年，即与Bohr-Landau定理的提出同一年，Hardy对Riemann猜想的研究也取得了突破性的结果。这便是我们在第一节中提到过的那个“令欧洲大陆数学界为之震动的成就”。在Riemann猜想的研究中，这一结果被称为Hardy定理[注一]：
　　
　　Hardy定理：Riemannζ函数有无穷多个非平凡零点位于临界线上。
　　
　　我们知道(详见上节)，无论Hadamard、Vallée-Poussin，还是Bohr、Landau，在Hardy之前人们所做的有关Riemann猜想的所有解析研究，都没能证明Riemannζ函数的哪怕一个非平凡零点落在临界线上。那时人们所知的有关临界线上的零点的全部结果只有我们在第八节中提到过的1903年Gram给出的15个零点以及1914年(与Hardy定理的提出同一年)Backlund计算出的79个零点。全部都是零星计算，且涉及的零点数目少得可怜。而忽然间，来自英伦岛上的Hardy居然不动声色地一举把临界线上的零点数目扩大到了无穷，不仅远远超过Backlund的区区79个零点，也永久性地超过了后世所能给出的任何具体的数值计算结果。因为无论用多么高明的计算方法，无论用多么强大的计算设备，也无论用多么漫长的计算时间，任何具体的数值计算所能验证的零点数目都是有限的，而无论多么大的有限数目相对于无穷来说都只是一个“零”。因此Hardy定理虽然没有给出临界线上任何一个具体零点的数值，但它通过对这些零点的存在性证明，为Riemann猜想提供了强有力的支持，并且超越了任何可能的具体数值计算[注二]。
　　
　　这样的一个结果出现在人们对Riemannζ函数的非平凡零点还知之甚少的1914年，而且还出现在与欧洲大陆数学界颇为疏离的英国，不能不令欧洲大陆的数学家们感到震动。
　　
　　Hardy定理的证明可以从一个有关ξ(s)的积分表达式：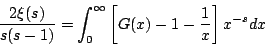

　　
　　入手。这里s的取值满足0<Re(s)<1，被积表达式中的函数G(x)则定义为：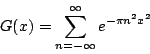

　　
　　我们在第五节中介绍过，ξ(s)的零点与Riemannζ函数的非平凡零点相重合，并且ξ(s)是一个整函数，性质比Riemannζ函数来得简单，从而在Riemann猜想的研究中是一个十分重要的辅助函数。证明Hardy定理的基本思路便是设法从前式中找出与ξ(s)在临界线上的零点分布有关的约束条件来。为此，第一步是从前式中解出G(x)-1-1/x。这与我们在第四节中介绍过的从lnζ(s)与J(x)的积分表达式中解出J(x)来是完全类似的，其结果也类似，为：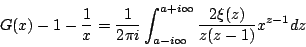

　　
　　其中积分上下限中的a满足0<a<1。从G(x)的定义中不难看到(读者可以自行证明)，G(x)在复平面上-π/4<Imln(x)<π/4的锲形区域内解析。进一步的研究还表明，在这一锲形区域的边界上G(x)存在奇点，特别是，当x从锲形区域内逼近i1/2(即eπi/4)时，G(x)及其所有导数都趋于零。
　　
　　另一方面，假如ξ(s)在临界线上只有有限多个零点，那么只要t足够大，ξ(1/2+it)的符号就将保持恒定(请读者想一想这是为什么？)。换句话说，只要t足够大，ξ(1/2+it)要么是恒正函数，要么是恒负函数[注三]。显然，t的这种大范围特征对上式右端的积分(积分限中的a取为1/2)会产生可观的影响。这种影响究竟有多大呢？Hardy经过研究发现，它足以破坏G(x)在x→i1/2时的所有导数都趋于零这一结果[注四]。这就表明ξ(s)在临界线上不可能只有有限多个零点——而这正是Hardy定理。
　　
　　

[1] [2] [3] [4] 下一页