Riemann 猜想漫谈 (十三)

作者：卢昌海
　　
　　在我们这Riemann猜想之旅的前面各节中，已先后介绍了Riemannζ函数的定义及其零点(尤其是非平凡零点)，非平凡零点与素数分布之间的关联，以及非平凡零点的计算(包括对其是否符合Riemann猜想的验证，以及数值计算)。沿着零点计算这一线索，我们介绍了人们对零点分布的统计研究，以及由此而发现的零点分布与物理之间出人意料的关联。这无疑是整个旅程中最令人惊叹的风景——事实上，我之所以萌生出写作这一系列的念头，这段风景乃是主要原因之一，因此，可以说正是这段风景使得我们的整个旅程成为可能。
　　
　　看过了这段风景，现在让我们重新回到纯数学的领地中来。从纯数学的角度讲，对一个数学猜想最直接的研究莫过于是寻求它的证明(或否证)，对Riemann猜想也是如此。可惜的是，Riemann猜想却一直顽固地抗拒着这种研究，直到今天为止，也还没有任何人能在这种研究上取得被数学界公认的成功。因此，我们所能介绍的只是数学家们试图逼近Riemann猜想——或者说逼近临界线——的过程。
　　
　　读者们想必还记得，在前面各节中，我们曾经介绍过两个具有普遍意义的零点分布结果：一个是第五节中提到的Riemannζ函数的所有非平凡零点都位于复平面上0≤Re(s)≤1的区域内。这是Euler乘积公式的一个简单推论(参阅附录一)；另一个则是第七节中提到的Riemannζ函数的所有非平凡零点都位于复平面上0<Re(s)<1的区域(即临界带)内。这是在证明素数定理的过程中由Hadamard与delaVallée-Poussin所证明的，比前一个结果略进了一步，时间则是1896年。这两个结果与Riemann猜想虽然还相距很远，但它们是普遍而严格的结果，适用于所有的非平凡零点，在这点上它们远远胜过了有关零点的所有数值计算。
　　
　　令人欣喜的是，在Hadamard与Vallée-Poussin之后“仅仅”过了十八个年头，即1914年，数学家们在对Riemannζ函数零点分布的研究上就又取得了两个重大进展[注一]。取得这两个重大进展的数学家正是我们在旅程伊始提到过的Hardy，Bohr和Landau。在本节中我们先来介绍Bohr与Landau的工作，即Bohr-Landau定理。
　　
　　但在介绍Bohr-Landau定理之前，让我们先对零点分布的基本对称性做一个简单分析。我们在第八节的注释中曾经提到，Riemannζ函数在上半复平面与下半复平面的非平凡零点是一一对应的。具体地讲，这种一一对应是通过以s=1/2(即实轴与临界线的交汇点)为原点的反演对称性实现的。这种对应性可以由零点与Riemannζ函数非平凡零点相重合的辅助函数ξ(s)所满足的关系式ξ(s)=ξ(1-s)(参阅第五节)看出来。除了这一反演对称性外，Riemannζ函数非的平凡零点分布还满足一个对称性，那就是关于实轴的反射对称性。这是由于ξ(s)除满足ξ(s)=ξ(1-s)外，还满足一个关系式：

(请读者自行证明)。由这两个对称性可以推知Riemannζ函数非平凡零点的分布相对于临界线也具有反射对称性。这些对称性的存在表明，要研究零点的分布，只需研究临界带的四分之一，即{Re(s)≥1/2,Im(s)≥0}的区域就行了。我们以前介绍过的零点计算就是针对这一区域的，下面要介绍的Bohr-Landau定理的表述也是如此。
　　
　　Bohr与Landau所证明的是这样一个定理[注二]：
　　
　　Bohr-Landau定理：如果|ζ(s)|2在直线Re(s)=σ上的平均值对σ>1/2有界，且对σ≥σ0>1/2一致有界，则对于任何δ>0，位于Re(s)≥1/2+δ的非平凡零点在全部非平凡零点中所占比例为无穷小。
　　
　　在进一步讨论这一定理之前，我们先来解释或定义一下该定理所涉及的一些术语的含义。首先解释一下什么叫做“|ζ(s)|2在直线Re(s)=σ上的平均值”。这个平均值是由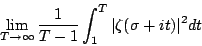

[1] [2] [3] 下一页