Riemann 猜想漫谈 (十三)

来定义的。这个定义与函数平均值的普遍定义——即函数在区间上的积分除以区间的长度——是完全一致的。只不过由于Re(s)=σ的长度无限，因此在定义中涉及到一个极限。此外由于我们真正关心的是t很大的区域，因此积分下限的选择并不重要，为了避免ζ(s)在s=1处的极点对定理的表述造成不必要的麻烦，我们选了一个非零的积分下限。
　　
　　其次，什么叫做|ζ(s)|2在直线Re(s)=σ上的平均值“对σ>1/2有界，且对σ≥σ0>1/2一致有界”？“对σ>1/2有界”很简单，就是说对任何σ>1/2，存在常数T0及C使得：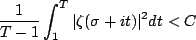

　　
　　对所有T>T0成立。而“对σ≥σ0>1/2一致有界”则是说对任何σ0>1/2，存在与σ无关的常数T0及C，使得上式对所有σ≥σ0及T>T0都成立。
　　
　　最后，“位于Re(s)≥1/2+δ的非平凡零点在全部非平凡零点中所占比例为无穷小”指的是位于{Re(s)≥1/2+δ,0≤t≤T}的非平凡零点的数目与位于{Re(s)≥1/2,0≤t≤T}的非平凡零点(即所考虑的临界带四分之一区域内0≤t≤T的全部非平凡零点)的数目之比在T→∞时趋于零[注三]。
　　
　　做了这些解释或定义，我们就对Bohr-Landau定理的字面含义有了一些了解。它实质上是在|ζ(s)|2的平均值与ζ(s)的零点分布之间建立了一种联系。这种存在于复变函数的模与零点之间的关联并不鲜见，1899年，丹麦数学家JohanJensen(1859-1925)提出的Jensen公式(Jensen'sFormula)及其推广Poisson–Jensen公式(Poisson–Jensenformula)就是一例，它把一个亚纯函数在一个圆域内的零点和极点与函数的模在圆域边界上的性质联系在了一起。这一公式也正是Bohr与Landau在证明他们的定理时所用到的主要公式。
　　
　　很明显，我们感兴趣的是Bohr-Landau定理中有关非平凡零点分布的叙述，即“对于任何δ>0，位于Re(s)≥1/2+δ的非平凡零点在全部非平凡零点中所占比例为无穷小”。但是这一叙述是否成立还有赖于Bohr-Landau定理的前提，即“|ζ(s)|2在直线Re(s)=σ上的平均值对σ>1/2有界，且对σ≥σ0>1/2一致有界”的成立与否。
　　
　　幸运的是，这一前提可以证明是成立的。为了看到这一点，我们来分析一个比较简单的情形，即σ≥σ0>1的情形。用我们在上文提到的关系式ξ(s)=ξ(s)，及σ>1时ζ(σ+it)的级数展开式Σnn-σ-it可得：
　　
　　|ζ(σ+it)|2=ζ(σ+it)ζ(σ-it)=ΣnΣmn-σ-itm-σ+it。
　　
　　另一方面，由于σ≥σ0>1时ζ(s)在s=1处的极点对计算没有影响，因此我们可以将|ζ(σ+it)|2的平均值定义中的积分下限取为-T(相应的将1/(T-1)改为1/(2T))以利于计算积分(这里再次用到了ξ(s)=ξ(s))。将上面有关|ζ(σ+it)|2双重求和表达式代入平均值的定义，并先交换积分与求和的顺序，再交换求和与极限T→∞的顺序(请读者自行证明这样做的合理性)，可以发现只有m=n的项才对结果有贡献，而它们的贡献一致收敛于Σnn-2σ=ζ(2σ)(也请读者自行证明)。这表明对所有σ≥σ0>1，Bohr-Landau定理中的前提都是成立的。
　　
　　当然，这样的简单证明不适用于σ≤1的情形(因为ζ(σ+it)的级数展开式不再适用)，但我们可以注意到证明结果中的ζ(2σ)对所有σ>1/2都有意义。因此读者们也许会猜测到这一结果的适用范围可以由σ≥σ0>1拓展到σ≥σ0>1/2。事实也正是如此。可以证明，对于任何σ0>1/2及ε>0，存在与σ无关的常数T0使得：

　　
　　对所有σ≥σ0及T>T0都成立。这一结果显然表明(请读者自行证明)Bohr-Landau定理中的前提是成立的。这一点在

上一页 [1] [2] [3] 下一页