成双成对的正弦定理和余弦定理 |
|
|
| 来源:不详 更新时间:2012-12-11 12:19:01 |
|
|
|
|
作者:学夫子
朋友们都知道正余弦定理,三角学里的一个历史悠久的公式。老实说从这哥俩的名字来想,我更愿意他们能够成双成对,但实际的公式除了有正余弦之分以外,貌似并无其他有联系之处。实际上,我们完全可以从另一个角度来看这两个定理,他们当真是成双成对的。
现有三角形ABC和高AD:
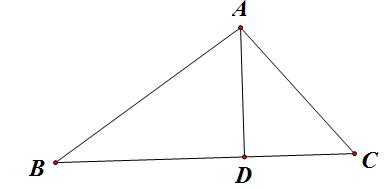
首先考虑边AB和AC在高AD上的投影,就能得到:
c×sinB=b×sinC
这样就得到了正弦定理。
现在再考虑边AB和AC在BC边上的投影(注意到AD和BC是互相垂直的方向,就如我们的坐标系一般),就能得到:
c×cosB+b×cosC=a…………①
①式就可以看做是余弦定理,不过这个公式因为涉及到5个量,所以并无多大用处,如果进行相应的对称替换,那一定有下面的式子成立:
a×cosB+b×cosA=c…………②
a×cosC+c×cosA=b…………③
将cosA、cosB和cosC看成未知数,那么①②③就构成一个三元一次方程组,解这个方程组既得:
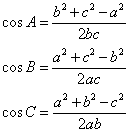
这就是我们的余弦定理了。经过这样的一个处理,正弦定理和余弦定理之间的关系就更加密切了:余弦定理就是将三角形两边朝着第三边投影后得到的结果,而正弦定理就是将三角形两边朝着第三边的高投影后得到的结果。(来源:学夫子数学博客)
|
上一个数学: 一个有关勾股定理的猜想
下一个数学: 数学公式变成几何图形 可以看、可以摸,还能讲故事 |
|
|
|
|
|
|
