,首先得有Riemannζ函数。只不过,Riemann猜想如果是“山寨版”的,作为其“核心部件”的Riemannζ函数当然也只需是“山寨版”的即可。这“山寨版”的Riemannζ函数从何而来呢?正是从有限域上的代数曲线中来。
为此,我们要引进有限域上代数曲线F(x,y)=0的一个重要性质,那就是它所含点的数目。这个性质之所以重要,因为它实际上就是有限域上代数方程F(x,y)=0的解的数目。如前所述,解的数目对于研究方程来说是一个重要课题,相应的,所含点的数目对于代数曲线来说也是一个重要性质。我们在前面说过,有限域Fq上的代数方程F(x,y)=0可以被视为是所有有限域Fqm(m=1,2,3,...)上的代数方程。用代数曲线的语言来说,这意味着有限域Fq上的代数曲线F(x,y)=0可以被视为是所有有限域Fqm(m=1,2,3,...)上的代数曲线。另一方面,代数曲线F(x,y)=0所含点的数目,或代数方程F(x,y)=0的解的数目,显然是与定义域Fqm的选取有关的。为了体现这种关系,我们用Nm表示定义域为Fqm时的这一数目。
有了这些准备,现在我们可以定义“山寨版”的Riemannζ函数了,那就是:
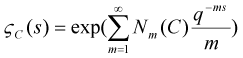
如此定义的“山寨版”Riemannζ函数与“正版”Riemannζ函数一样,是关于复变量s的函数,它有一个比较正式的名字,叫做有限域上代数曲线的ζ函数。在这一函数的定义中,我们特意引进了一个表示代数曲线的字母C,因为此定义所给出的函数显然与代数曲线的选取有关;定义中的q则来自于代数曲线C的原始定义域Fq中的q(q不出现在左侧,是因为表示代数曲线的C已经包含了Fq这一定义域信息,从而包含了q)。
有了“山寨版”的Riemannζ函数,我们就可以表述有关其零点分布的“山寨版”Riemann猜想了。由于这个猜想是关于有限域上代数曲线的ζ函数零点分布的,因此我们称其为有限域上代数曲线的“山寨版”Riemann猜想。
有限域上代数曲线的“山寨版”Riemann猜想:有限域上代数曲线的ζ函数的所有零点都位于复平面上Re(s)=1/2的直线上。
由于“山寨版”Riemannζ函数与代数曲线的选取有关,而后者有无穷多种,因此上述“山寨版”Riemann猜想实际上是无穷多个猜想的统称。对于特定的代数曲线及原始定义域,该猜想可以通过对“山寨版”Riemannζ函数的直接计算加以验证,有些甚至是相当容易的,但涵盖所有代数曲线及原始定义域的普遍证明却大为不易。
我们在上节中曾经提到,Weil并不是“山寨版”Riemann猜想这一研究方向的开创者。事实上,早在1923年,奥地利数学家EmilArtin(1898-1962)就提出了有限域上一类被称为超椭圆曲线(hyperellipticcurve)的特殊代数曲线上的ζ函数,以及相应的“山寨版”Riemann猜想[注六]。1933年,德国数学家HelmutHasse(1898-1979)则证明了有限域上一类被称为椭圆曲线(ellipticcurve)的特殊代数曲线上的“山寨版”Riemann猜想(请注意,Artin只是提出猜想,Hasse则是证明猜想,而且两人所针对的是不同情形下的猜想——前者针对超椭圆曲线,后者针对椭圆曲线)[注七]。
Artin的猜想及Hasse的证明虽都有一定的广泛性(各自都涵盖了无穷多的个例),但针对的仍只是特定类型的代数曲线。Weil的贡献则在于给出了上述“山寨版”Riemann猜想的普遍证明(即针对任意代数曲线的证明)。不过,在上节提到的他给Cartan的信件中,他给出的只是证明的大致思路,完整的证明直到二战结束后的1948年才发表。Weil对“山寨版”Riemann猜想的贡献还不止于此。完成了对上述猜想的证明后的第二年,即1949年,Weil对该猜想进行了一次重要推广。这个推广的证明是如此困难,不仅他自己未能给出,在接下来二十四年的时间里,参与研究的所有其他数学家也都未能给出完全的证明。他的这一推广因此而被称为了Weil猜想(Weilconjectures)。
Weil猜想包含了若干个命题,“山寨版”Riemann猜想是其中之一,并且从历史上讲是证明最为不易的一个上一页 [1] [2] [3] [4] [5] 下一页
|
