作者:学夫子
在《从黄金分割比推菲波拉契数列》一文中。我们谈到,可以通过黄金分割比的连分数来倒推菲波拉契数列,以看清菲波拉契数列和黄金分割比之间的本质关系,要用到的,就是连分数的概念。为了方便,在这里提一下:
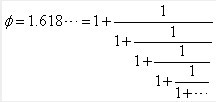
得到连分数以后,在某一步停止,就得到逐渐趋近于原数的一系列收敛子的有理分数:
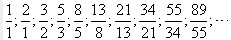
这些分数都交替性地趋近于1.618……而我们发现,上面的分子和分母都是一组菲波拉契数列,让我们知道,原来是黄金分割比产生了菲波拉契数列,不过今天我们将要来看,其实,任何数的连分数,其实从一个角度,都是和菲波拉契数列有关系的。
假设数可以写成下面的连分数形式
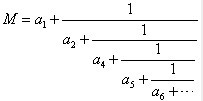
一般情况下我们为了美观,我们写成下面的浓缩形式:
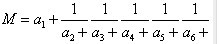
相应的可以得到一系列近似值的有理分数,其中ak称之为该连分数的第k个商数,现在我们有下面的性质:
如果有连续三个有理分数分别为p/q,r/s,t/v,那么:
r/s=(p-t)/(q-v)
也就是说,对于连续的三个收敛子,第一个与第三个的分子和分母分别相减,得到的分数等于中间的分数。不过,得到的分数并不是(p-t)/(q-v),而需要将它进行约分。化到最简……比如我们最喜欢最神秘的圆周率π的收敛子:
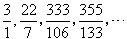
我们可以用非常巧妙的办法来证明这个结论,设连续的第一个分数为m,我们现在将m看成原数的“整数部分”,若第二个分数所对应的商数为ak,第三个分数所对应的商数为ak+1,那么这三个分数就是:
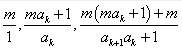
利用这组式子,就可以证明我们上面的结论。并且我们发现:
性质1:如果ak+1等于1,那么中间分数的分母就是前后两个数的分母之差,分子就是前后两个分数的分子之差,而无需约分;如果ak+1不等于1,那么就需要约掉ak+1。这就促使我们这样去想,如果在所有的收敛子中,都不涉及到约分,那么任何一个分数的分母就是前两个分数的分母之和,分子就是分子之和……那么所有分母或者分子这不就是传说中的菲波拉契数列么?根据我们前面的分析,要想实现这样的效果,就必须使得所有的ak+1都等于1,而这,就刚好是我们的黄金分割比的连分数:
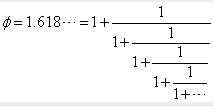
[1] [2] 下一页
