原来黄金分割比之所以能够产生菲波拉契数列,是因为他连分数的所有商都是1!
利用性质1,我们可以根据一个数连分数的展开形式,快速写出这个数的有理分数,比如π,在上面我们已经写出其前四个有理分数:
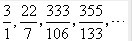
我们现在来写第五个有理分数:
要写第五个有理分数,先通过其连分数展开式中,第五个商为25:
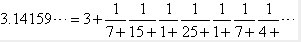
由于第五个连分数的分母减去第三个的分母,等于第四个的分母乘以25,分子也是一样,所以,第五个有理分数应该是:
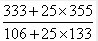
然后化简就行,往后可以按照这个办法继续做。都知道老祖宗祖冲之得出了“密率”和“疏率”,很多学生知其然不知其所以然,通过连分数,大伙应该有所了解,我们上面的有理分数中,22/7就是疏率,355/133就是密率。通过连分数,你可以得到密得多的密率。(来源:学夫子数学博客)
上一页 [1] [2]
