a.苏珊有一个问题,她上学时总遇到斯蒂克。
斯蒂克:喂,苏珊。我和你一起走好吗?
苏珊:讨厌,走开。
b.苏珊:我有主意了,我每天早上上学都走不同的路,斯蒂克就找不到我了。
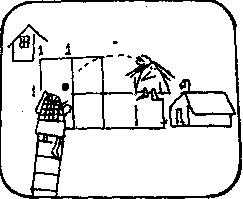
c.这个图表示苏珊家和学校间的所有街道,图中苏珊上学这条路不是向东就是向南。
d.这是苏珊上学的另一条路,到底有多少条路?

e.苏珊:我想知道到底我能走几条路,我想这很难算。嗨!一点儿也不难,太简单了!苏珊想到什么办法了?
f.苏珊:我在住处所在的角标上1,因为只有一个起点。再在这个角相邻的两个角标上1,因为只有1条路能到达。
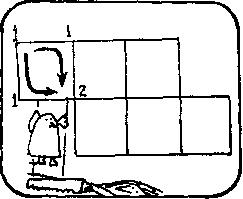
g.苏珊:现在我把2标在这个角上,因为我能通过两条路到达这里。
当苏珊意识到2是1加1的和时,她突然想到每个角的数字一定是相邻能到达这个角的两角的数字和。
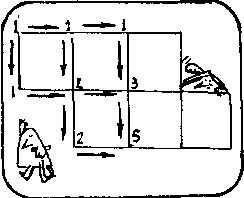
h.苏珊:已经标出了几个角,我马上就会标上其它角。
你能为苏珊标上其它角并告诉她上学能走几条路吗?
多少条路?
剩下的五个顶点,从上至下,从左到右应标上1,4,9,4和13,最后一个顶点的13表示苏珊按最短路径有13条路去上学。
苏珊的发现的确是计算学上最短径数的简单快捷的算法。如果她试图画出所有路径,再数它们那就太繁杂了,而且当街道网络量大时也是根本办不到的。当你实际画一下13条路径时,你会更好地体验算法的有效性。
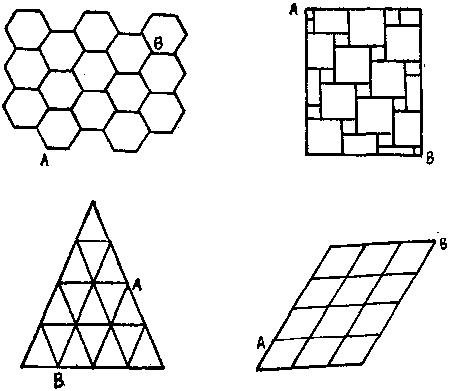
图1
为了检验你对这种算法的理解程度,试着画一下其它几种街道网络,并应用这种算法确定从顶点A到顶点B的最短路径的数量。图1给了这种类型的四个同题,它们也可用其它方法求解,如使用组合数学的公式,但这种方法太复杂了。
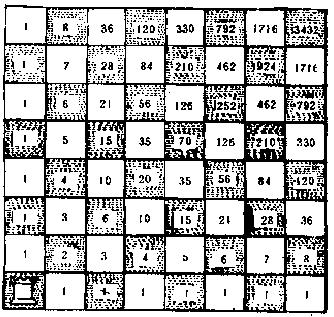
图2
国际象棋中的车从棋盘的一角到达对角线另一角的最短路径数是多少呢?根据苏珊为街道标号的方法,通过为每个棋格标号很快就可解决。因为车只能沿直角(水平和垂直)移动,所以最短路径只能限制在向目标方向的移动上,如图2所示,整个棋盘已正确标记,标号马上就给出了从起始区域到盘上任何其它区域的最短路径数。右上
角格中的数字是3432,所以车从一角沿对角线到另一角的最短路径数是3432条。
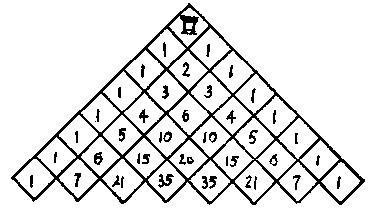
图3
把棋盘沿对角线切成一半,然后转动成为图3所示的三角形。底排格中的数字就是从顶点到底排各格的最短路径数。这个三角形的标号和著名的帕斯卡三角形①中的数字是相等的。
这种从顶到底最短路径的算法,准确地构成了帕斯卡三角形,这种同构的精确推 广,就是帕斯卡三角形的迷人之处。由帕斯卡三角形马上就可得到二项式展开式各项的系数和一些基本概率问题的解答。注意图3中从三角形顶端到底部外边格中数字都是1,越往中心移数字越大,或许你见到过这种按帕斯卡三角形原理构造的装置,一块倾斜的板,几百个小球沿着桶滚入板底各栏、球准确地按漏斗型二项式函数曲线排列,这是因为进入每个口的最短路径致都是二项展开式的系数。
苏珊算法同样适用于具有长体小格的立方体。想一想,边长3个单位的立方体被分为27个小立方体,有一个车在一个小格中,车可以沿三个座标方向平等移动,它沿着空间对角线到达另一端的最短路径数是多少呢?
————————
①中国人称之为杨辉三角,系中国南宋数学家杨辉发现。
