动量守恒定律是高考考查的热点问题,每年考题都涉及该部分内容,题型也较广泛,因此,认真学好动量守恒定律是高中理科学生所必须的.关于动量守恒定律的基本形式及成立的条件在高中物理选修课中已有详细的叙述和讨论,在这里不再多说.在实际问题的处理中,经常遇到一些问题,其满足动量守恒条件,但却不能用动量守恒定律的基本形式m1v1+m2v2=m1v1′+m2v2′来解决.例如常见的人船模型,这种情况用动量守恒定律的推论来解决就显得非常必要了.我认为用下面这种方法来向学生阐述此推论是比较合理的,教学实践证明,这种方式学生也非常容易接受,这比起用平均速度来阐述要合适得多.现叙述如下,供同行们参考.
高中阶段对动量守恒定律的应用基本上仅限于一维运动的情况,所以整个过程中速度都在同一条直线上.动量守恒的数学表达式为:p0=m1v2+m2v2.设整个系统中只有两个物体(高中阶段最常见).根据动量守恒定律的相对性可知,式中的速度v1、v2及p0都是相对于同一参照系而言的,通常都是以地球为参照系.动量守恒定律也具有同时性,动量守恒定律两边动量分别是系统在初、末态的总动量,初态的动量中的v10,v20是指相互作用前同一时刻两物体的瞬时速度,末态动量中的v1,v2是相互作用后同一时刻的瞬时速度.由此可知在人船模型中是不能简单套用公式的.
例1如图1所示,船在平静的水面上,不计水的阻力,人从船头走向船尾时,问船的位移是多少?(设船长为l,人的质量为m,船的质量为M).
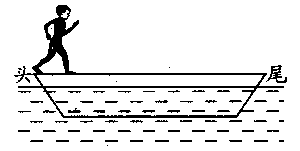
图1
分析把船和人当做系统,则系统所受的合外力为零,人在行走时,系统时时刻刻都满足动量守恒的条件,即
p0=mv1+Mv2,①
其中v1、v2代表任一时刻人、船的瞬时速度.
在①式两边同时乘以一个极短的时间,因为时间极短,可以认为在这极短的时间内人和船的速度都是匀速的,所以速度与时间乘积可看成是这段时间内的位移Δs1、Δs2,
即p0Δt=mv1Δt+Mv2Δt,
p0Δt=mΔs1+MΔs2,
把所有的位移Δs1,Δs2分别加起来,有
p0∑Δt=m∑Δs1+M∑Δs2,②
∑Δt是全过程所用时间t,∑Δs1是人所经过的位移s1,∑Δs2是船所经过的位移s2,s1、s2都是在时间t内完成的,当然也是相对于同一参照系的,因为速度v1,v2都是相对于同一参系的.将②改写为
p0t=ms1+Ms2,③
即为本文所述的动量守恒定律的有用推论.
讨论1.p0=0时,ms1+Ms2=0;
2.p0≠0时,t=(ms1+Ms2)/p0.
高中阶段所讨论的问题大多是p0=0的情况.
现再回到前面例题所提出的问题.根据动量守恒定律,有
0=ms1+Ms2,
式中s1不是l,因为s1表示人对地的位移,即s1地=s1人船+s船地=(l+s2),
代入上式,得
0=m(l+s2)+Ms2,s2=-ml/(M+m).
所以,船的位移与人行走的方向向反,大小为ml/(M+m).用上面所述方法来阐述动量守恒定律的推论,会使学生加深对动量守恒定律相对性特别是同时性的理解,教学实践表明,这种讲述形式是成功的,在所教班级中学生基本上都能很自如地解决此类问题.
例2载人的汽球原来静止在离地面高为h的空中,汽球质量为M,质量为m的人要沿气球上的绳梯着地,如图2所示,则绳梯长度至少为多长?
[1] [2] 下一页
